Reference no: EM131031

1. Joe and Sam each invested $20,000 in the stock market. Joe's investment increased in value by 5% per year for 10 years. Sam's investment decreased in value by 5% for 5 years and then increased by 12.5% for the next 5 years. AT the end of 10 years, what was the value of each person's investment?

2. Investigate the following functions for both horizontal and vertical asymptotes, x and y-intercepts, and state the domain and range of each and where the function is increasing and decreasing.     

(A)  f(x) = (2x³ - 3x - 5)/(x³ - 8).                                                            (B) g(x) = (x - 3)/(x² - 5x  + 6)

3. A manufacturing company wants to package its product in a rectangular box with a square base and a volume of 32 cubic inches. The cost of the material used for the top is $.05 square inch; the cost of the material used for the bottom is $.15 per square inch, and the cost of the material used for four sides is $.10 per square inch. What are the dimensions of the box with the minimum cost?

4. In planning a restaurant, it is estimated that a revenue of $6 per seat will be realized if the number of seats is at most 50. On the other hand, the revenue on each seat will decrease by $.10 for each seat exceeding 50 seats. Find the revenue function where x = the number of seats exceeding 50 seats. What is the maximum revenue and what number of seats generates that maximum revenue.

5. You invest $1,000 at an annual interest rate of 5% compounded continuously. How much is your balance after 8.5 years?  How long will it take you to accrue a balance of $4,000? What interest rate is required to yield a balance of $7,000 after 7 years?

6. A sum of $2,500 is deposited in a bank account that pays 5.25% interest compounded weekly. How long will it take for the deposit to double?  How long will it take you to accrue a balance of $7,500?  What interest rate is required to yield a balance of $7,000 after 7 years?

7. Solve the following logarithmic equations. A) log(x-1)  - log(x+1) = 1; B) ln(x) = -1.147; C) ln(x) =  (2/3)ln(8) + (1/2)ln(9) - ln(6); D) log₅ (x) + log₅ (x-4) = log₅ (21);  E) log₄ (3x) - log₄ (x²-1) = log₄ (2)

8. Solve the following exponential equations. A) 3^(7x+1) =  3^(4x-5); B) 8^x  =  2^(x-6); C)  3^(x+2) = 5: D)  4^(x) = 2^(3x+4); E) e^{(x - 6)} = 3.5.

9. Graph f(x) = 2^x - 3 and approximate the zero of f to the nearest tenth. Also find the y-intercept and any horizontal and vertical asymptotes.

10. In a research experiment, a population of fruit flies is increasing according to the law of exponential growth. After 2 days there are 100 flies, and after 4 days there are 300 flies. How many flies will there be after 5 days?16. Differentiate the following functions using the limit definition:

Part A. f(x) = x²+x-5; Part B. f(x) = (4x+100); Part C. f(x) = 3/(x+4)

11. Find the following limits.
A

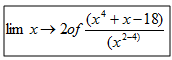
Part A denominator should be (x² - 4) not (x^2-4)