Reference no: EM13520

1. Let Tn be the nth Chebyshev polynomial

Tn(x) = cos(n cos^-1x); x∈2 [-1; 1]; n = 0; 1,......

Show that the polynomials de ned by

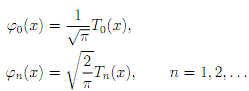
form a system of orthonormal polynomials with respect to w(x) = (1 x²)^-1/2 on the interval ( -1, 1).

2. Write a Matlab function M- le called phicoeff.m to evaluate the coecients of the polynomials ' φ₀, φ₁, .........φ_n' using the three term recurrence relation

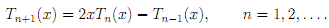
Your function should have n as the only argument and return an (n+1)(n+1) matrix whose rows are the vectors containing the coecients of the polynomials in the standard Matlab format for polynomials (see the documentation of the built-in function polyval).

3. Use phicoeff.m and the Matlab built-in function polyval to evaluate the polynomials '0; : : : ; '5 at 1000 points in the interval [ 1; 1]. Plot '0; : : : ; '5 on the same gure.

4. Write a Matlab function M- le called trapezium.m to approximate the integral b a f(x) dx using the composite Trapezium pricipal. Your function could have the following arguments: the function handle for the function f, the two real numbers a, b and the number of strips used in the composite Trapezium rule.

5. Let I be the composite Trapezium rule (with m strips) for the integral

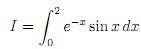
Let E_m = |I - I_m|. Find I analytically, using integration by parts twice. Furthermore, give an analytical bound for the error Em. Use trapezium.m, to evaluate Em numerically for m = 10; 50; 100; 500; 1000; 5000; 10000 and print your results with 5 digits of accuracy. Use the built-in function loglog to plot, on the same gure, Em and its analytical bound as functions of m.

6. Let L_w²( -1, 1) be the linear space of all real-valued functions f de ned on ( -1, 1) and such that w(x)|(x)|² is integrable on ( -1; 1). Let h
;
i be the following inner product on L_w²( 1; 1)

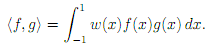
Further, let w and 'φ_n, n =0,1....... be de ned as in Question 1. Show that the following formula holds true

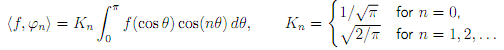
7. Let w be the weight function of Question 1 and let f be the de ned as

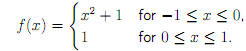
Further, let pn be the polynomial of best approximation of degree n to the function f L_w²( -1, 1) in the 2-norm on the interval (-1; 1). Calculate approximately the polynomials p3, p5 at 200 points in the interval [-1; 1].