Reference no: EM13562
1. Consider the production function:
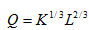
where Q is total output, K is the amount of capital used, and L is the amount of labor used.
a. Derive the marginal product functions for both K and L.
b. In the short run, with K fixed, does this production function exhibit diminishing marginal returns to labor?
c. Demonstrate whether or not this production function generates convex isoquants.
d. Demonstrate that the production function exhibits constant returns to scale.
2. True or False, Explain: In the short run, when total product is rising, the marginal product of labor must be increasing.
3. Consider a short run production function where K is fixed and L is variable. Output rises from zero at a constant rate up until 10 units of L are used. Beyond that, output rises at a decreasing rate up until 30 units of L are used. Using more than 30 units of L causes output to decline.
a. Diagram the short run total product function.
b. Diagram the marginal product and average product of labor functions.
4. Can a production function be consistent with the law of diminishing marginal returns and increasing returns to scale? Explain why or why not.
5. A firm's production function is given by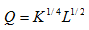 
. Assume w = $20 and r=$10.
a. Derive the firm's demand functions for K and L .
b. Derive the long run total, average, and marginal cost functions.
6. A firm's production function is given by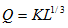 
. Assume w = $27, r = $18, and K is fixed at 3 units.
a. Derive the firm's short run demand for L.
b. Derive the short run total cost (SRTC) function.
c. Derive the SRMC, SRAVC, and SRATC functions.
7. Generally, the cost minimizing combination of K and L to produce any level of output occurs where:
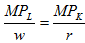
Fully explain why.
8. Suppose a firm adopted a new capital saving technological innovation. How would this affect the firm's long run expansion path. Explain.
9. True or False, Explain: Increasing returns to scale implies that a firm can increase its long run output while reducing its long run total costs of production.
10. Suppose that the total cost of providing satellite television services is given by:
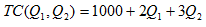
where Q1 and Q2 are the number of households that subscribe to a sports channel and movie channel, respectively. Does the provision of satellite television services exhibit economies of scope?