Assume that the amount of money in a bank account after t years is specified by,

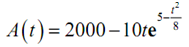
Find out the minimum & maximum amount of money in the account throughout the first 10 years that it is open.

Solution: Here we are actually asking for the absolute extrema of A(t) within the interval [0,10]. As with the earlier examples this function is continuous everywhere and thus we know that this can be done.

First we'll require the derivative thus we can determine the critical points.

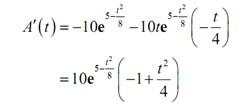
The derivative presents everywhere and the exponential is never zero. So the derivative will only be zero where,

-1 + (t²/4)   = 0           ⇒         t ²  = 4          ⇒            t = ±2

We've obtained two critical points, however only t = 2 is in fact in the interval so that is just critical point that we'll utilizes.

Now let's evaluate the function at the lone critical point & the end points of the interval.  Following are those function evaluations.

A (0) = 2000           A ( 2) = 199.66               A (10) = 1999.94

 Thus, the maximum amount in the account will be $2000 that takes places at t = 0 and the minimum amount in the account will be $199.66 that occurs at the 2 year mark.