Derivatives of Hyperbolic Functions : The last set of functions which we're going to be looking at is the hyperbolic functions.  In several physical situations combinations of e^x and e^{- x} arise fairly frequently.  Due to this these combinations are given names.  There are six hyperbolic functions & they are described as follows.

sinh x = e^x - e^{- x}/2                                   cosh x = e+ + e^{- x} /2

tanh x = sinh x /cosh x                    coth x = cosh x /sinh x =1/tanh x

sech x =1/cosh x                                    csch x = 1/sinh x

Following are the graphs of the three main hyperbolic functions.

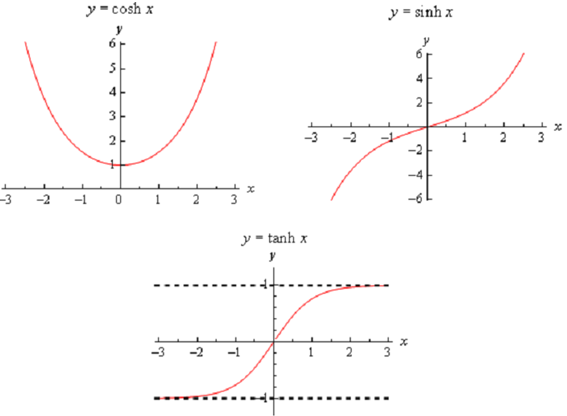
We also contain the following facts regarding the hyperbolic functions.

sinh ( - x ) =- sinh ( x )                                        cosh ( - x ) = cosh ( x )

cosh ² (x ) - sinh ² ( x ) = 1                                        1 - tanh ² ( x ) = sech ² ( x )

You'll note as well that these are identical, but not quite the similar, to some of the more common trig identities so be careful to not confuse the identities here  along with those of the standard trig functions.

Since the hyperbolic functions are described in terms of exponential functions determining their derivatives are rather simple provided already. However we haven't thus we'll required the following formula.

                                                                 d (e^{- x} )/ dx= -e^{- x}

Along with this formula we'll do the derivative for hyperbolic sine

d (sinh x)/ dx   = d((e^x - e^{- x}  )/2)/ dx = e^x -(- e^{- x} ) /2 = (e^x + e^{- x}  )/2= cosh x

For the rest we can either utilizes the definition of the hyperbolic function and/or the quotient rule. Following are all six derivatives.

d (sinh x ) /dx = cosh x                                  d (cosh x ) / dx = sinh x

d ( tanh x ) /dx = sech ² x                               d (coth x )/dx =-csch ² x

d (sech x )/dx = -sech x tanh x                         d (csch x ) /dx= -csch x coth x