Reference no: EM132389458
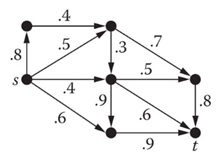
Assignment: 1. Suppose that the weighted graph shown below represents a communication network, where the weight pij on arc ij is the probability that the link from i to j does not fail. If the link failures are independent of one another, then the probability that a path does not fail is the product of the link probabilities for that path. Under this assumption, find the most reliable path from s to t. (Hint: Consider - log10pij.)
2. Suppose that a set E of jobs are to be processed by a single machine. All jobs require the same processing time, and each job has a deadline. A subset of jobs is said to be manageable if there is a processing sequence for the jobs in the subset, such that each job is completed on time. Show that (E, I) is a matroid.
3. What is the maximum number of edges in a simple graph with a DFS-tree isomorphic to K1,5. Prove your answer.
4. Show that if no two edges of a connected graph G have the same weight, then the minimum spanning tree is unique. Either draw a graph meeting the specifications or explain why no such graph exists.
5. 6-vertex graph G such that κv(G) = 2 and κe(G) = 2.
6. Determine the vertex- and edge-connectivity of the complete bipartite graph Km,n.
7. Prove that there exists no 3-connected simple graph with exactly seven edges.
8. Prove that if a graph has exactly two vertices of odd degree, then there must be a path between them.
9. Let T be a tree with at least three vertices, and let T∗ be the subtree of T obtained by deleting from T all its vertices of degree 1. Prove that diam(T∗) = diam(T) - 2 and rad(T∗) = rad(T) - 1.
10. Determine the smallest integer n ≥ 2 for which there exists an n-vertex tree whose only automorphism is the trivial one.
a. Prove that every path is graceful.
b. Prove that K1,n(also called a star) is graceful for all n ≥ 2.
c. Show that every tree on 6 vertices is graceful.
d. Prove or disprove: Every tree is graceful. (This is an open problem.)
11. Definition: The distance sum (or Wiener index†) of a graph G, denoted ds(G), is
12. The sum of the distances between all pairs of vertices in G; that is, ds(G) =
13. Determine the distance sum for the n-vertex star K1,n-1.
14. Let T be an n-vertex tree different from the star K1,n. Prove that ds(T) > ds(K1,n-1)
15. Determine the distance sum for the n-vertex path graph Pn.
16. Let T be an n-vertex tree different from the path graph Pn. Prove that ds(T) <ds(Pn).