Reference no: EM13907

Problem 1:

In a study relating college grade point average to time spent in various activities, students are asked how many hours they spend each
week in four activities: studying, sleeping, working, and leisure. Any activity is put into one of the four categories, so that for each
student the sum of hours in the four activities must be 168. The regression model is given by

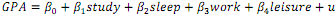
a) Does it make sense to hold sleep, work, and leisure fixed while changing study? Why or why not?

b) Explain why this model violates the assumption of no perfect collinearity.

c) How could you reformulate the model so that its parameters have a useful interpretation and it satisfies the no perfect collinearity assumption?

Problem 2:

The following equation describes the median housing price in a community in terms of the amount of pollution (nox, for nitrous oxide) and the average number of rooms in houses (rooms).

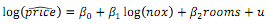
a) What are the probable signs of beta1 and beta2? What is the interpretation of beta1? Explain. Assume that the following equations were estimated based on this model:

b) Why might nox and rooms be negatively correlated? If this is the case, does the simple regression of log(price) on log(nox) produce an upward or downward biased estimator of beta1? Explain.

c) Is the relationship between the simple and multiple regression estimates of the elasticity of price with respect to nox what you would have predicted given your answer in part (b)? Why or why not?

Problem 3:

Consider an equation to explain salaries of CEOs in terms of annual firm sales, return on equity (ROE, in percent form), and return on the firm's stock (ROS, in percent form):

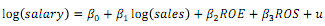
a) In terms of model parameters, state the null hypothesis that, after controlling for sales and ROE, ROS has no effect on CEO salary.

State the alternative that better stock market performance (higher ROS) increases a CEO's salary.

Assume the following was estimated based on this model from a sample of 209 firms where the standard errors are given in  parentheses:

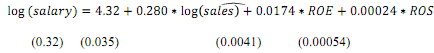
b) By what percent is salary predicted to increase, if ROS increases by 50 points?

c) Test the hypothesis that ROS has a positive effect. Carry out the test at the 10% significance level.

d) Test the hypothesis that a 1% increase in sales implies a less than 1% increase in CEO salary at the 5% significance level.

Problem 4:

This problem refers to Doughtery's Educational Attainment and Earnings Functions (EAEF) data set, accessible through the course  website. This data is a subset of the U.S. National Longitudinal Study of Youth 1979 (NLSY79). It is a nationally representative panel survey of young people aged 14 to 21 in 1979. Participants were surveyed annually from 1979-1994 and every other year afterwards. The EAEF subsample is made up of 22 randomly selected subsets of 540 individuals each (270 men and 270 women).

Examples in the text use subset 21. Use subset 1 for this problem. The following is a summary of the variables needed for this problem.

S Years of schooling (highest grade completed as of 2002) ASVABC Composite score on the ASVAB, a standardized test of numerical and verbal ability with a mean of 50 and standard deviation of 10 ASVAB02 Score on the arithmetic reasoning section of the ASVAB test ASVAB03 Score on the word knowledge section of the ASVAB test ASVAB04 Score on the paragraph comprehension section of the ASVAB test SM Years of schooling of respondent's mother SF EXP EARNINGS Years of schooling of respondent's father Total work experience in years Current hourly earnings in $ a) Using the data set, regress S on SM, SF, ASVAB02, ASVAB03, and ASVAB04 (3 components of the ASVABC composite score).

a. Report your coefficient estimates and standard errors. (You may simply submit your output for this part.)

b. Compare the coefficients and standard errors from part (a) to those from a regression of S on SM, SF, and ASVABC. Explain any differences.

c. Calculate correlation coefficients for the three ASVAB components.

b) Regress the logarithm of earnings on S and EXP. (You will need to create the new variable log(EARNINGS).) Interpret the regression results.

c) Assume that ASVABC is a measure of a person's ability that we expect to be positively correlated with S.

a. Regress S on ASVABC and SM. Interpret the coefficients and comment on their statistical significance.

b. Regress S on ASVABC only. Interpret the slope coefficient and comment on the statistical significance.

c. Regress S on SM only. Interpret the slope coefficient and comment on the statistical significance.

d. Compare the coefficients of ASVABC in the regressions from parts (a) and (b). Give mathematical and intuitive explanations of direction of the change.

e. Compare the coefficients of SM in the regressions from parts (a) and (c) and explain the direction of the change.