Estimation of difference among two means

We know that the standard error of a sample is given by the value of the standard deviation (σ) divided by the square root of the number of items in the sample (√n).

However, when given two samples, the standard errors is described by

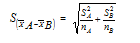
Also note that we do calculate approximately the interval not from the mean although from the difference between the two samples means that is: (x¯_A - x¯_B)

The appropriate number of confidence level does not change

Thus the confidence interval is described by:

 (x¯_A - x¯_B) ± Confidence level S_{(x¯A - x¯B)}

=  (x¯_A - x¯_B)  ± Z  S_{(x¯A - x¯B)}

Illustration

Given two samples A and B of 100 and 400 items respectively, they contain the means x¯₁= 7 ad x¯₂ = 10 and standard deviations of 2 and 3 respectively. Construct confidence interval at 70 percent confidence level?

Solution

Sample                        A                                  B

                               x¯₁ =      7                      x¯₂= 10

                               n₁ = 100                       n₂ = 400

                               S₁ = 2                           S₂ = 3

The standard error of the samples A and B is described by:

S_{(x¯A - x¯B)} = √{(4/100) + (9/400)}

= ¼ = 0.25

At 70 percent confidence level, then appropriate number is equal to 1.04 or as read from the normal tables

(x¯₁ - x¯₂)= 7 - 10 = - 3 = 3

We take the absolute value of the difference among the means for illustration, the value of   x¯ = absolute value of X that is a positive value of X.

Therefore Confidence interval is described by:

= 3± 1.04 (0.25 )          From the normal tables a z value of 1.04 provide a value of 0.7.

= 3± 0.26

= 3.26 and 2.974

Hence 2.974 ≤ X ≤ 3.26