Compute the maximum bending moment:

A simply supported beam of 7 m length carries point loads 2 kN, 4 kN and 6 kN at distances of 1 m, 2 m & 4 m from the fixed end respectively. Draw BMD & SFD and also compute the maximum bending moment that will take place.

Solution

By taking moments around A to find RB,

R_B × 7 - (6 × 4) - (4 × 2) - (2 × 1) = 0

Therefore,        R_B = 4.857 kN, and

R_A = 12 - 4.857 = 7.143 kN

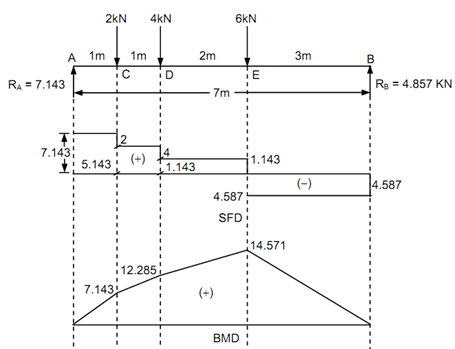
Shear Force (Starting from left end A)

 SF at A, F_A = + 7.143 kN

SF just left of C = + 7.143 kN

SF just right of C = + 7.143 - 2 = + 5.143 kN

SF just left of D = + 5.143 kN

SF just right of D = + 5.143 - 4 = + 1.143 kN

SF just left of E = + 1.143 kN

SF just right of E = + 1.143 - 6 = - 4.857 kN

SF just left of E = - 4.857 kN = Reaction at B

Bending Moment (Starting from right end B) BM at A, MA = 0

BM at E, M_E = + 4.857 × 3 = + 14.571 kN m

BM at D, M_D = + (4.857 × 5) - (6 × 2) = + 12.285 kN m

BM at C, M_C  = + (4.857 × 6) - (6 × 3) - (4 × 1) = + 7.142 kN m

Or        M_C = 7.143 × 1 = + 7.143 kN m   (considering left side)

BM at A,  M_A = 0

Figure

Maximum bending moment shall occur at a point where the shear force changes sign. Here, SF alters from positive to negative at E. The Bending Moment at E shall be maximum bending moment.

Thus,   M_max = + 14.571 kN m