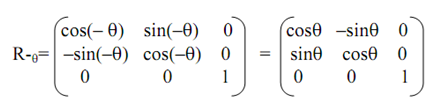Rotation about the origin - 2-d and 3-d transformations

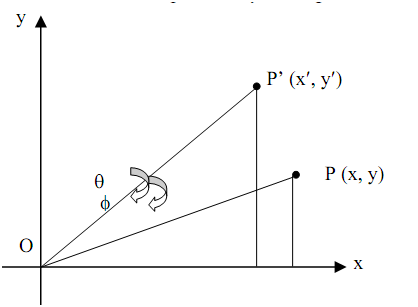
Specified a 2-D point P(x,y), which we need to rotate, along with respect to the origin O. The vector OP has a length 'r' and making a +ive or anticlockwise angle φ with respect to x-axis.

 Suppose P' (x'y') be the outcome of rotation of point P by an angle θ regarding the origin that is demonstrated in Figure 3.

P(x,y) = P(r.cos φ,r.sin φ)

P'(x',y')=P[r.cos(φ+ θ),rsin(φ+ θ)]

The coordinates of P' are as:

x'=r.cos(θ+ φ)=r(cos θ cos φ -sin θ sin φ)

=x.cos θ -y.sin θ     (where x=rcosφ and y=rsinφ)

As like;

y'= rsin(θ+ φ)=r(sinθ cosφ + cosθ.sinφ)

=xsinθ+ycosθ

Hence,

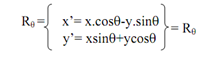
Hence, we have acquired the new coordinate of point P after the rotation. Within matrix form, the transformation relation among P' and P is specified by:

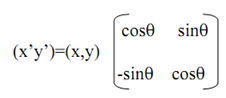
There is P'=P.R_q                                               ---------(5)

Here P'and P represents object points in 2-Dimentional Euclidean system and R_q is transformation matrix for anti-clockwise Rotation.

In terms of Homogeneous Coordinates system, equation (5) becomes as

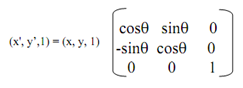
There is P'h=Ph.R_q,                                                     ---------(7)

Here P'h and Ph   represent object points, after and before needed transformation, in Homogeneous Coordinates and R_q is termed as homogeneous transformation matrix for anticlockwise  or =ive Rotation. Hence, P'h, the new coordinates of a transformed object, can be determined by multiplying previous object coordinate matrix, Ph, along with the transformation matrix for Rotation R_q.

Keep in mind that for clockwise rotation we have to put q = -q, hence the rotation matrix R_q , in Homogeneous Coordinates system, becomes: