Power Series and Functions

We opened the previous section by saying that we were going to start thinking about applications of series and after that promptly spent the section talking about convergence again.  In fact it is now time to start with the applications of series.

Along with this section we will start talking about how to denote functions with power series.  The usual question of why we might want to do this will be answered in a couple of sections one time we actually learn how to do this.

 Let us start off with one that we already know how to do, even though while we first ran across this series we didn't think of it as a power series nor did we acknowledge that it denoted a function.

Remind that the geometric series is 

Don't forget also that if |r| ≥  1 the series diverges.

Now here, if we take a = 1 and r = x this becomes,

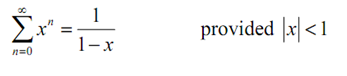
Turning this around we can see that we can denote the function

f (x) = 1/ (1-x)

with the power series

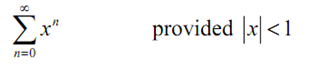
This provision is significant.  We can clearly plug any number other than x = 1 into the function, however, we will just only get a convergent power series if |x| < 1.  The meaning of this is that the equality in (1) will only hold if |x| < 1.  For any other value of x the equality would not hold.  Note as well that we can as well make use of this to acknowledge that the radius of convergence of this power series is R = 1 and the interval of convergence is |x| < 1.

This plan of convergence is important here.  We will be presenting several functions as power series and it will be significant to recognize that the representations will frequently only be valid for a range of x's and that there might be values of x that we can plug into the function that we cannot plug into the power series representation.