While we first looked at mechanical vibrations we looked at a particular mass hanging on a spring with the possibility of both a damper or/and external force acting upon the mass. Now there we want to look at the subsequent situation.
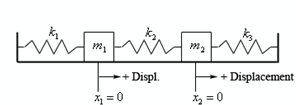
In the above figure above we are assuming that the system is in rest. Conversely, all three springs are now at their natural lengths and are not exerting any forces on either of the two masses and which there are no now any external forces acting upon either mass.
We will use the subsequent assumptions regarding to this situation once we start the system in motion.
1. x1 will measure the displacement of mass m1 from its equilibrium which is resting position and x2 will measure the displacement of mass m2 from its equilibrium position.
2. As noticed in the figure above all displacement will be supposed to be positive if this is to the right of equilibrium position and negative if to the left of the equilibrium place.
3. Each force acting to the right is positive forces and each force acting to the left is negative forces.
4. The spring constants, k1, k2, and k3, are all positive and may or may not be similar value.
5. The surface of the system is sitting on is frictionless and therefore the mass of each of the objects will not influence the system in any way.
Before writing down the system for this case recalls which the force exerted through the spring upon the each mass is the spring constant times the amount which the spring has been stretched or compressed and we'll require being careful along with signs to ensure that the force is acting in the right direction.