Inverse Cosine : Now see at inverse cosine.  Following is the definition for the inverse cosine.

                        y = cos^-1 x       ⇔ cos y = x                   for     0 ≤ y ≤ ?

As with the inverse since we've got a restriction on the angles, y, which we get out of the inverse cosine function. Again, if you'd like to verify it a quick sketch of unit circle should convince you that this range will cover all possible values of cosine exactly once.  Also, we have

                          -1 ≤ x ≤ 1 because -1 ≤ cos ( y ) ≤ 1.

Example   Evaluate cos^-1   (-√2/  2)

Solution : As with the inverse sine we are actually just asking the following.

                                                       cos y = - √2 /2

where y have to meet the requirements given above.  From a unit circle we can illustrates that we must have y =3 ∏/4    .

The inverse cosine & cosine functions are also inverses of each other and therefore we have,

cos (cos^-1  x ) = x                                          cos^-1 (cos x ) =x

To determine the derivative we'll do the similar kind of work which we did with the inverse sine above.  If we begin with then,

                                                     f ( x ) = cos x          g ( x ) = cos^-1 x

then

g ′ ( x ) =1/f ′ ( g ( x )) = 1/- sin (cos^-1  x )

Here Simplifying the denominator is almost alike to the work we did for the inverse sine & so isn't illustrated here.  Upon simplifying we get the given derivative.

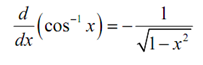
Therefore, the derivative of the inverse cosine is closely identical to the derivative of the inverse sine. The single difference is the negative sign.