Find out the joint distribution:

Let X_I and X₂ be two independent random variables each distributed uniformly in the interval [ 0, a ], where a > 0 is a constant. Find out the joint distribution of

Y_l = X_l + X₂ and Y₂ = X₁ - X₂.

Instead, in vector notation, what is the distribution of Y = XA.

where

x = (X₁,X₂),Y= (Y₁,Y₂), A = 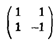? Find also the marginal distributions of Y₁ and Y₂. ?

Solution:

The joint pdf of X is

f_x(x) = 1/a², (x₁,x₂)? R(x)

= 0 otherwise.

Where

R(x) = {(x₁,x₂):0 ≤ x₁ ≤ a, 0 ≤  x₂ ≤ a}

The Jacobian of the transformation is

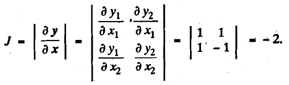
Hence the pdf of Y is

f_y(y) = 1/2a², (y₁,y₂)? R(y)

= 0 otherwise.

where R ( y ) is the transformed region R ( x ) under the transformation Y = XA. The range of variation of Y_l is clearly [ 0,2a ] and that of Y₂ is [ - a, + a ]. However Y_l and Y₂ are not independent.

Since the inverse transformation is

X₁= ½ (Y₁ + Y₂), X₂ = ½ (Y₁ - Y₂) and 0≤ x₁, x₂ ≤ a,

the region R ( y ) is given by

R(y) = {( Y₁ + Y₂) : 0 ≤ Y₁ + Y₂ ≤ 2a, 0≤ Y₁ - Y₂ ≤2a},

The Relation between R ( x ) and R ( y ) is illustrated in Figure 2.

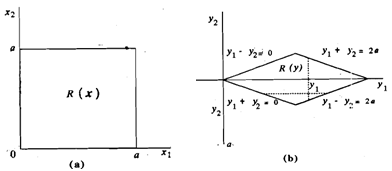
Figure: Relation between R ( x ) and R ( y ).

Note that the variables x_l and x₂ are independent and the region R ( x ) is such that for X_l - x_l, the variation X₂ does not depend on x_l, but the region R ( Y ) is not of that type and the transformed variables Y_l and Y₂ are not independent.

The variable Y_l varies in the interval [ 0, 2a]and for a fixed y_l, if 0≤ y₁≤ a, then y₂ takes on values -y₁≤y₂≤ y₁, while, if a< y₁≤ 2a then y₂ varies in the interval

-(2a-y₁) <.y₂ ≤ (2a - y₁)

Integrating f_y ( y ) with respect to y₂, the marginal pdf of y₂ is obtained as follows

f_Y1(y1) = 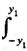1/2a² dy₂ = y₁/a², for 0 ≤ y1 ≤ a

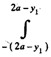1/2a² dy₂  = 2a-y₁/a², for a< y₁ ≤ 2a

= 0 otherwise.

In a similar manner, we note that for a given Y₂, if -a ≤ y₂ ≤ 0 then

-y₂ ≤ y₁ ≤ 2a-y₂, and if 0≤ y₂ ≤ a then y₂ ≤ y₁ ≤ 2a - y₂

Hence,

f_Y2(y₂) = 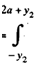1/2a² dy₁ = a+y₂/a², -a ≤ y² ≤ 0

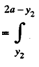1/2a² dy₁ = a-y₂/a² , 0< y² ≤ a

= 0 otherwise.

Remarks:

The forms of pdf the marginal distributions In Example 5 are shown in Figure 3. Due to their triangular shape of pdf's, the distributions are called triangular distributions.

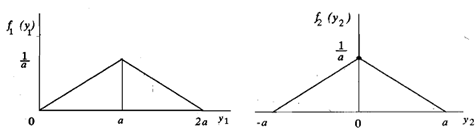
Figure: The forms of the marginal distributions of Y_I and Y₂