Consider the line segment AB in 3-Dimentional parallel to the z-axis along with end points A (- 5,4,2) and also B (5,-6,18). Carry out a perspective projection upon the X=0 plane; here the eye is placed at (10, 0,10).

Solution: Suppose here that P (x, y, z) be any point in the space.

The parametric equation of a line beginning from E and passing via P is: E + t. (P - E), o < t < 1.

= (10,0,10) + t. [(x, y, z) - (10, 0, 10)]

= (10, 0,10) + t [(x - 10)], y (z - 10)]

= (t. (x - 10) + 10, t. y, t (z - 10) + 10)

Suppose a point P' can be obtained, as t = t*

∴P' = (x', y', z') = (t* (x - 10) + 10, t*.y, t*. (z - 10) + 10)

 Because the point P' lies on x = 0 plane as:

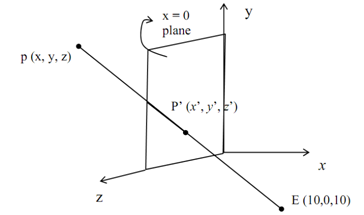
          Figure: (j)

= t* (x - 10) + 10 = 0

= t* =(- 10)/ (x - 10)

= P' = (x',y',z') = (0,((-10.y)/(x - 10)),(((-10)(z - 10))/(x - 10)), + 10)

(0, ((-10.y)/(x - 10)),((10x - 10z)/(x - 10)))

In terms of Homogeneous coordinate system;

P' = (x', y', z', 1) = ( 0, ((-y )/((x - 10) - 1)) ,  (x -z)/((x/10) - 1)), 1)

= (0, -y, x-z, ((x/10) - 1))

In Matrix form there is:

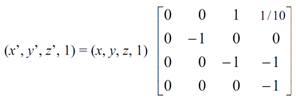
-------------------------(1)

In above equation (1) is the needed perspective transformation, that gives a coordinates of a projected point P' (x', y', z') on the x = 0 plane, whereas a point p (x, y, z) is viewed from E (10, 0, 10)

Currently, for the specified points A (-5, 4, 2) and B (5, -6, 18), A' and B' are their projection upon the x = 0 plane.

So now from Equation (1) we get:

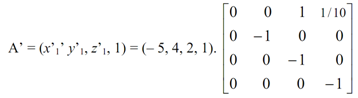
= (0,-4, -7, ((-5/10) - 1))

= (0 , -40, -70, -15)

(0, 40/15, 70/15, 1)

Thus x₁' = 0;  y₁' = 2.67 ;    z₁' = 4.67

As the same in:

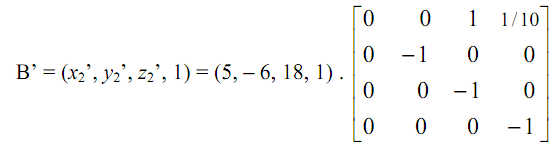
= (0, 60, - 130, - 5)

= (0, - 12, 26, 1)

 Thus x₂' = 0 ;  y₂' = - 12 ;    z₂' = 26

Hence the projected points A' and B' of specified points A and B are:

A' = (x1', y1'z1') = (0, 2.67, 4.67)    and     B' = (x2', y2', z2') = (0, - 12, 26, 1)