Arc Length with Parametric Equations

In the earlier sections we have looked at a couple of Calculus I topics in terms of parametric equations.  We now require to look at a parametric equations.

In this part we will look at the arc length of the parametric curve illustrated by,

x = f (t)

y = g (t)

α ≤ t ≤ β

We will as well be assuming that the curve is traced out exactly one time as t increases from α to β.  We will as well need to suppose that the curve is traced out from left to right as t increases. This is equal to saying,

dx/dt  ≥ 0        for  α ≤ t ≤ β

Thus, let's begin the derivation by recalling the arc length formula since we first derived it in the arc length part of the Applications of Integrals chapter.

L = ∫ ds

In which,

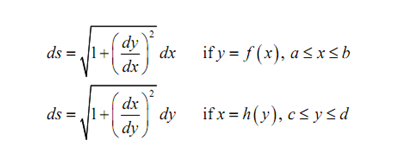
We will make use of the first ds above since we have a nice formula for the derivative in terms of the parametric equations. To make use of this we'll as well need to know that,

 dx = f ′ (t) dt = (dx/dt) dt

After that the arc length formula becomes,

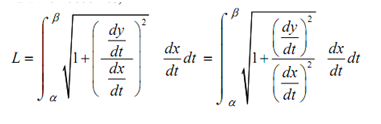
This is a specifically unpleasant formula.  Though, if we factor out the denominator from the square root we reach at,

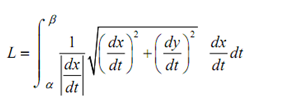
Here now, utilizing our assumption that the curve is being traced out from left to right we can drop the absolute value bars on the derivative that will permit us to cancel the two derivatives that are outside the square root.