Reference no: EM13969676

Problem 1: Mathematical Background: Set Theory

1. Let A = {1,2,3}, B = {∅,{1},{2}}, and C = {1,2,{1,2}}. Compute A ∪ B, A ∩ B, B ∩ C, A ∩ C, A × B,

A × C, C \ B, A × B × C, and 2B. Recall that 2A denotes the power set of A, and A \ B denotes A set difference B.

2. Prove that for any sets A, B, and C, A × (B ∪ C) = (A × B) ∪ (A × C).

Problem 2 Mathematical Background: Proofs and Induction

1. Prove Pythagorean Theorem, which states that the square of hypotenuse is equal to the sum of squares of the other two sides.

2. Prove by contradiction that there are infinitely many prime numbers.

3. Suppose that a post office sells only 2¢ and 3¢ stamps. Show that any postage of 2¢, or over, can be paid for only using these stamps.

Problem 3 Propositional Logic

1. Prove that the following semanic entailments are true by using truth tables.
• (p → q) → r,s → ¬p,t,¬s,t → q |= r
• ∅ |= q → (p → (p → (q → p)))

2. Prove the following inferences in propositional logic using natural deduction proof rules.
• (p → q) → r,s → ¬p,t,¬s,t → q ` r
• `q → (p → (p → (q → p)))

Problem 4 [Complexity of Some Problems in Propositional Logic]

Two of the commonly used normal forms for formulas in propositional logic is Conjunctive Normal Form (CNF) and Disjuctive Normal Form (DNF). A formula φ is said to be in k-CNF form if it is a conjuction of subformulas, i.e., φ = ψ₁∧ψ₂∧ψ_l where, each ψ_i is a disjuction of k literals, i.e., ψ_i = p₁∨p₂ ∨...∨pk. A formula ξ is said to be in k-DNF if it is a disjunction of subformulas, i.e, ξ = η₁∨η₂ ∨...∨η_l where, each η_i is a conjunction of k literals, i.e., η_i = p₁ ∧ p₂ ∧...∧p_k. Here, p_i can be a propositional variable or its negation. Now prove the following complexity theoretical problems over propositional logic.

1. Given a k-DNF formula, prove that its satisfiability can be decided in polynomial time.

2. Given a k-CNF formula, prove that to decide whether the given formula is a tautologycan be decided in polynomial time.

3. Given a 2-CNF formula, prove that its satisfiability can be decided in polynomial time.

Problem 5 [Solving Sudoku Using SAT Solvers] Sudoku is a popular number-placement puzzle that originated in France in the end of the 19th century. Modern Sudoku was likely invented by Howard Garns from Connersville, Indiana and was first published in 1979 under the name Number Place. The objective of the puzzle is to place numbers 19 on a 9×9 grid, such that each number occurs only once in every row, every column, and every of the nine 3×3 subgrids that compose the main grid. Sudoku puzzles are grids that have been partially occupied with numbers. The task is then to occupy the remaining fields in such a way that the constraints on rows, columns, and sub-grids are satisfied. A sample Sudoku problem and its solution are given in Figure 1. For more information about Sudoku refer to its Wikipedia page at https://en.wikipedia.org/wiki/Sudoku.

In this problem, you will use one of the SAT Solvers Z3 (downloadable at https://z3. codeplex.com/ and use Python API) or use MiniSAT (downloadable at https://minisat.se/ with C++ API) to solve the sudoku problem given in Figure 1. Alternatively, you can also you use any other SAT solver of your preference. In this problem, you will do the following:

1. Write the boolean formula for the constraints that each number can occur at most oncein every row.

2. Write the boolean formula for the constraints that each number can occur at most oncein every column.

3. Write the boolean formula for the constraints that each number can occur at most oncein every 3×3 sub-grid.

Encode each of the above mentioned constraints using the API for the solver that you chose. Finally, encode the constraints which specify the numbers provided in the partially filled puzzle.

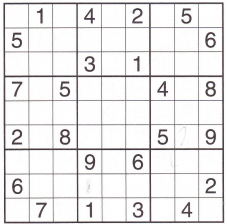
Figure 1: Sudoku puzzle for Problem 5.