Reference no: EM132369222
Discrete Mathematics Assignment -
Q1. The logical connective "NOT OR", denoted by ↓, is true only when neither p nor q are true.
(a) Write down the truth table for p ↓ q.
(b) Write down the truth table for (p ↓ q) ↓ (p ↓ q). What do you notice?
(c) Show that both negation, as well as AND, can be written using only ↓s.
Q2. Suppose we are considering all computers at Macquarie. Let P (x) be the statement "x is connected to the network" and let Q(x) be the statement "x has at least 100 Terabytes of storage". Express each of the following sentences in terms of P (x), Q(x), quantifiers, and logical connectives.
(a) No computer at Macquarie is connected to the network, and also has at least 100 Terabytes of storage.
(b) There is a computer at Macquarie which is connected to the network, and has at least 100 Terabytes of storage.
(c) There is a computer at Macquarie which is either not connected to the network or has less than 100 Terabytes of storage.
Q3. Let P (x, y) be the proposition x2 = y, where x and y are in the universe of integers.
Determine the truth value of each of the following propositions.
(a) ∃x P (6, x)
(b) ∃x P (x, 6)
(c) ∀x ∃y P (x, y)
(d) ∃y ∀x P (x, y)
Q4. Prove or disprove each of the following propositions.
(a) If n2 is a multiple of 4, then n is a multiple of 4.
(b) If n3 is a multiple of 2, then n is a multiple of 2.
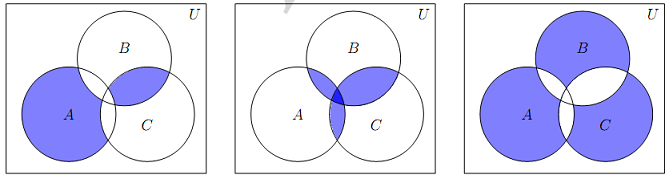
Q5. Write down expressions for each of the shaded regions.
Q6. Suppose a relation is symmetric and transitive. Does that automatically make it reflexive? If so, explain why. If not, give a counterexample.
Q7. The following adjacency table for an undirected graph G is missing some information.
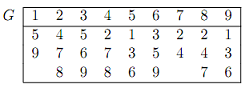
Explain how you could detect that it cannot possibly be complete. Correct it by adding the minimal possible extra information, and then determine the number of connected components in the graph, and the vertices in each connected component.
Q8. Determine the number of vertices for a simple graph which has 10 edges, two vertices of degree 4 and all the other vertices of degree 3. Sketch an example of such a graph. Is it planar? (There may be several non-isomorphic solutions.)
Q9. Decide whether the two graphs G1 and G2 are equivalent, given their adjacency matrices as below.

If not, explain why they cannot be equivalent. If so, draw the graph and label each vertex with the label of the row it corresponds to in the first matrix in blue and the label of the row it corresponds to in the second matrix in red.
Q10. Seven towns labelled A, B, C, D, E, F and G are connected by a system of freeways as follows:
(i) F1 goes from A to E, passing through D;
(ii) F2 goes from E to G and then passes through D as it continues to F;
(iii) F3 goes from G through C to A;
(iv) F4 goes form F to D, passing through B;
(v) F5 goes from B to G.
Each freeway permits travel in both directions.
(a) Using vertices for towns and edges for freeway sections between towns, draw a graph which models this situation.
(b) List all the simple∗ paths from E to F, which do not pass through any city more than once.
(c) What is the smallest number of freeway sections which would need to be closed to prevent travel from D to G?
Q11. (a) Prove that G = (V,E) has no Eulerian walk, where the vertices are V = { a, b, c, d, e, f } and the edges are E = { ab, ac, bc, bd, ce, de, df, ef }.
Show that it is possible to add one edge to G to form a simple graph that does have an Eulerian walk, and find such a walk. There may be more than one way to do this.
(b) Show that G = (V,E) has no Hamiltonian cycle, where the vertices are V = { a, b, c, d, e, f, g } and the edges are E = { ab, ac, bc, bd, cd, de, df, ef, eg, fg }.
Q12. What is wrong with the following "proof" by Mathematical Induction?
We will prove statements that all computers are built by the same manufacturer. In particular, we prove statements B(n) with n ∈ N, that "in any collection of n computers, all of the computers are built by the same manufacturer".
First check that B(1) is true, since with only one computer there is only one manufacturer. Now assume B(k); that is, in any collection of k computers, all are built by the same manufacturer.
To prove B(k + 1) consider any collection of k + 1 computers. Pull out one of these computers, 'HAL' say, leaving just k computers, all of which must have the same manufacturer.
Swap the 'HAL' computer with one of the others, so again there are k computers, so all must have the same manufacturer. Thus 'HAL' must have the same manufacturer as the others, hence all k + 1 computers have the same manufacturer; that is B(k + 1) must be true.