Reference no: EM131445946

Mathematical Problems in Industry Assignment

Q1. Consider the one-dimensional steady state heat equation

(k(x)u')' = -f(x)                                                                 (1)

on the interval 0 ≤ x ≤ 1 with the boundary conditions

u = 0 at x = 0 and - ku' = h(u - 1) at x = 1.

This corresponds to internal heat production of f per unit length per unit time, with a fixed temperature boundary condition at x = 0 and a cooling boundary condition at x = 1 (with external temperature being taken as 1.)

For simplicity take k = 1, f = 1 and h = 1. (So, in particular, k and f do not depend on x.)

(a) Multiply (1) by a suitable test function and intergrate by parts to obtain the weak formulation of this problem. Be careful to specify any boundary conditions that might apply to the spaces of trial and test functions. What is the bilinear form a(. , .) and the functional f(.) in this case?

(b) Let W0 be a finite dimensonal subspace of the full space in (a). What is the approximate weak formulation corresponding to W₀?

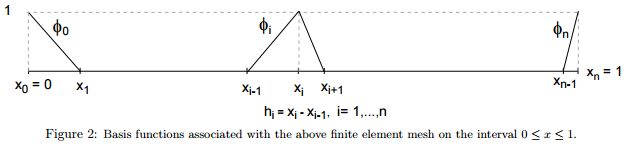
(c) Consider the one-dimensional finite element mesh on [0, 1] shown below.

Let W be the finite element subspace of continuous, piecewise linear functions defined for this mesh, and let φ_i, i = 0, . . . , n be the corresponding linear Lagrange basis functions of W.

In this case W₀ = {w ∈ W : w = 0 at x = 0}. Write down a set of basis functions for W₀ in terms of the φ_i.

(d) Write down the approximate version of the weak formulation in terms of these basis functions. (Hint: Express the approximate solution as a sum of basis functions with unknown scalar coefficients. Then use each of the basis functions in turn as the test function in (b).)

(e) Explicitly evaluate all of the stiffness matrix elements a(φ_i, φ_j) and the load vector components f(φ_j) that arise in (d). Your answer should be expressed in terms of the quantities hi defined in Figure 1. (Hint: It is convenient to consider the cases where the test function φ_j corresponds to a node x_j that lies in the interior of the interval (j = 1, . . . , n - 1) separately from the cases where the test function φ_j corresponds to a node that is on the boundary of the interval (j = 0 and j = n.)

(f) If the boundary condition u = 0 at x = 0 is changed to u = 1, for example, how would your answers to the above questions change? (Hint: Write the unknown solution w as w = u + U^˜, where u = 0 at x = 0 and U^˜ is some (arbitrary) extension of the boundary condition u = 1 at x = 0 to the entire interval [0, 1]. We could take U˜ = 1 everywhere as that extension; however, for this problem it is convenient to instead take U^˜ = φ₀.)

Attachment:- Assignment Files.rar