Reference no: EM131012897

Assignment

1. A nuclear reactor has created 18 grams of a particular radioactive isotope. Every hour 1% of this radioactive isotope decays.

a) Set up a recurrence relation for the amount of this isotope left n hours after its creation.

b) What are the initial conditions for the recurrence rela-tion in part (a)?

c) Solve this recurrence relation.

2. Suppose that every hour there are two new bacteria in a colony for each bacterium that was present the previous hour, and that all bacteria 2 hours old die. The colony starts with 100 new bacteria.

a) Set up a recurrence relation for the number of bacteria present after n hours.

b) What is the solution of this recurrence relation?

c) When will the colony contain more than 1 million bac-teria?

3. A small post office has only 4-cent stamps, 6-cent stamps, and 10-cent stamps. Find a recurrence relation for the number of ways to form postage of n cents with these stamps if the order that the stamps are used mat¬ters. What are the initial conditions for this recurrence relation?

4. Find the solutions of the simultaneous system of recurrence relations

an = a_n-1 + b_n-1

bn = a_n-1 - b_n-1

with a₀ = 1 and b₀ = 2.

5. Let L(i, j) denote the length of a longest common subsequence of a₁, a₂,....... a_i and b₁, b₂,......b_j, where 0 ≤ i ≤ m and 0 ≤ j ≤ n. Use parts (a) and (b) of Exercise 15 to show that L(i, j) satisfies the recurrence relation L(i, j) = L(i -1, j - 1) + 1 if both i and j are nonzero and a_i = b₁, and L(i, j) = max(L,(i, j - 1), L(i - 1, j)) if both i and j are nonzero and a_i ≠ b_i, and the initial condition L(i, j) = 0 if i = 0 or j = 0.

6. Develop an algorithm for finding a longest common subsequence of two sequences a₁, a₂,....... , a_m and b₁, b₂,...... b_n, using the values L(i, j) found by the algorithm in Exercise 17.

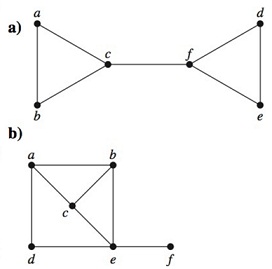
In Exercises find the number of vertices, the number of edges, and the degree of each vertex in the given undirected graph. Identify all isolated and pendant vertices.

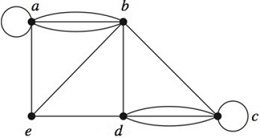
7. Find the sum of the degrees of the vertices of each graph in Exercises 1-3 and verify that it equals twice the number of edges in the graph.

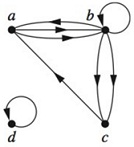
In Exercises determine the number of vertices and edges and find the in-degree and out-degree of each vertex for the given directed multigraph.

8. What does the degree of a vertex in the Hollywood graph represent? What does the neighborhood of a vertex repre¬sent? What do the isolated and pendant vertices represent?

9. Draw these graphs.

a) K_1,8

b) C₇

c) W₇

10. How many subgraphs with at least one vertex does K₂ have?

11. How many subgraphs with at least one vertex does W₃ have?

12. If G is a simple graph with 15 edges and G^- has 13 edges, how many vertices does G have?

In Exercises determine whether the given pair of graphs is isomorphic. Exhibit an isomorphism or provide a rigorous argument that none exists.

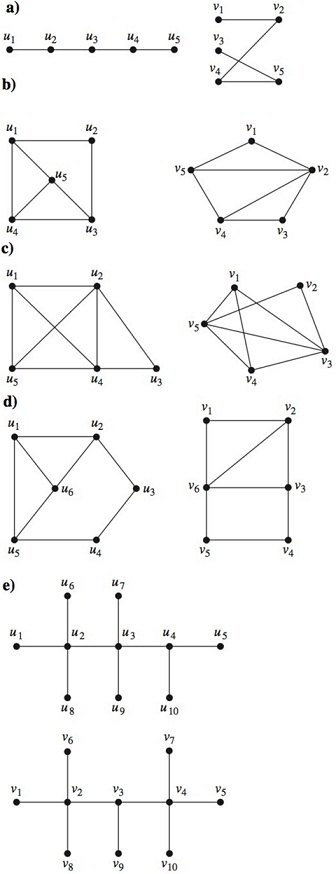
14. How many nonisomorphic simple graphs are there with n vertices, when n is

a) 2? b) 3? c) 4?

15. How many nonisomorphic simple graphs are there with six vertices and four edges?

In Exercises determine whether the given pair of di-rected graphs are isomorphic.

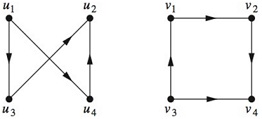
17. How many nonisomorphic directed simple graphs are there with n vertices, when n is

a) 2? b) 3? c) 4?

18. Does each of these lists of vertices form a path in the following graph? Which paths are simple? Which are suits? What What are the lengths of those that are paths?

a) a, b, e, c, b      b) a, d, a, d, a

c) a, d, b, e,a      d) a, b, e,c, b, d, a

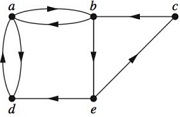
19. In Exercises determine whether the given graph is connected.

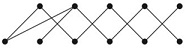
20. How many connected components does each of the graphs in Exercises 3-5 have? For each graph find each of its connected components.

21. Determine whether each of these graphs is strongly con-nected and if not, whether it is weakly connected.

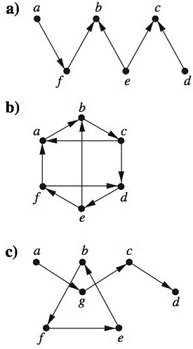
22. Find the number of paths of length n between any two ad-jacent vertices in K_3,3 for the values of n in Exercise.

Exercise- Find the number of paths of length n between two different vertices in K₄ if n is

a) 2. b) 3. c) 4. d) 5.

23. In Exercises determine whether the given graph has an Euler circuit. Construct such a circuit when one exists. If no Euler circuit exists, determine whether the graph has an Euler path and construct such a path if one exists.

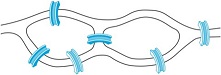
24. Can someone cross all the bridges shown in this map ex-actly once and return to the starting point?

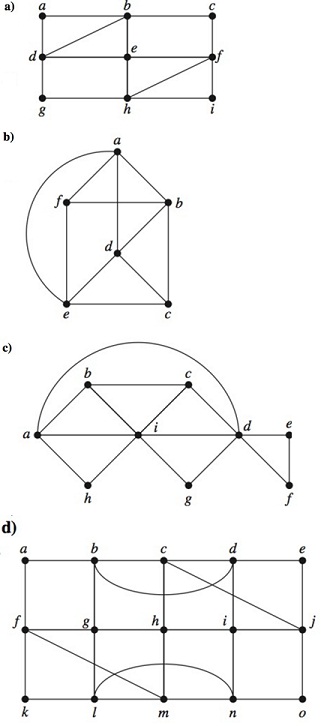
25. For which values of n do these graphs have an Euler circuit?

a) K_n b) C_n c) W_n d) Q_n

26. In Exercises determine whether the given graph has a Hamilton circuit. If it does, find such a circuit. If it does not, give an argument to show why no such circuit exists.