Reference no: EM131000797

1. Let y(x) satisfies the initial value problem (x²+y)dx = x dy, y(1)=2, then y(3) =?

(a) 2

(b) 3

(c) 12

(d) 9

2. Let d₁ and d₂ denote the usual metric and the discrete metric on R respectively. Let f:(R,d₁)→(R,d₂) be defined by f(x)=x, x∈ R. Then

(a) f is continuous but f^-1 is not continuous

(b) f^-1 is continuous but f is not continuous

(c) both f and f^-1 are continuous

(d) neither f nor f^-1 is continuous

3. The inverse of Laplace transform of 2s²-4/(s-3)(s²-s-2) is

(a) (1+t)e^-t +(7/2) e^-3t

(b) 2t + te^-t +(1/3) e^t

(c) (7/2) e^3t - (1/6) e^-t - (4/3) e^2t

(d) (7/2) e^-3t - (1/6) e^t - (4/3) e^-2t

4. Let trace (P)=1 and det (P)=-6, where P is a 2x2 matrix. Then trace (P⁴-P³)

(a) 78

(b) 97

(c) 6

(d) 1

5. Let T:R⁴→ R⁴ be linear map defined by T(x, y, z, w)=(x+z,2x+y+3z,2y+2z,w). Then the rank of T is equal to

(a) 4

(b) 3

(c) 2

(d) 1

6. Let G={e,x,x²,x³,y,xy,x²y,x³y} with o(x)=4, o(y)=2 and xy=yx³. Then the number of elements in the center of the group G is equal to

(a) 4

(b) 8

(c) 2

(d) 1

7. The possible set of eigen values of a 6x6 skew-symmetric orthogonal real matrix is

(a) {±i}

(b) {±i, ±1}

(c) {±1}

(d) {0, ±i}

8. The number of group homomorphism from Z₃ to Z₉ is

(a) 3

(b) 9

(c) 27

(d) 6

9. Let G be a group of order 231. The number of elements of order 11 in G is      

(a) 21

(b) 11

(c) 10

(d) 1

10. Let

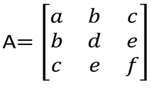
be a real matrix with eigenvalues 1,0, and 3. If the eigenvectors corresponding to 1 and 0 are (1,1,1)^T and (1.-1,0)^T respectively then the value of 12f =

(a) 28

(b) 1

(c) 7

(d) 14

11. Let u(x, y)=2f(y)cos(x-2y), (x, y)∈R², be a solution of the initial value problem 2u_x+u_y=u , u(x,0)= cos(x). Then f(1)=

(a) ½

(b) e/2

(c) e

(d) 3e/2

12. Let p(x) be the polynomial of degree at most 3 that passes through the points (-2,12),(-1,1),(0,2) and (2,-8). Then the coefficient of x³ in p(x)=

(a) -3

(b) -2

(c) 1

(d) -1

13. Let M be a 3x3 matrix with 1,2 and 3 as eigenvalues. If M^-1 = (M²/α) - M + (11/α)I₃, for some scalar α ≠ 0, then α =

(a) 47

(b) 6

(c) 5/6

(d) 47/6

14. If the trapezoidal with single interval [0,1] is exact for approximating the integral ₀∫¹(x³ - cx²) dx, then the value of c=

(a) 3

(b) 1.5

(c) 6

(d) -3

15. The number of non-isomorphic abelian groups of order 24 is               

(a) 3

(b) 15

(c) 6

(d) 24

16. Five teams have to compete in a league, with every team playing every other team exactly once, before going to the next round. How many matches will have to be held to complete the league round of matches?

(a) 20

(b) 10

(c) 8

(d) 5

17. Let M be 3 x3 real matrix such that

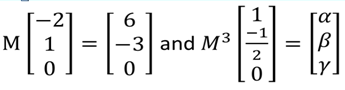. Then|α|=

(a) 27

(b) 18

(c) 36

(d) 2/9

18. If for some α, β ∈ R, the integration formula, ₀∫² p(x) = p(α) +p(β) hold for all polynomials p(x) of degree at most 3, then the value of 3(α-β)²=

(a) 12

(b) 4

(c) 3

(d) 0

19. Which of the following groups has a proper subgroup that is not cyclic?

(a) Z₁₅ x Z₇₇

(b) S₃

(c) (Z,+)

(d) (Q,+)

20. If

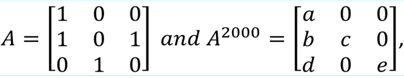, then (a,b,c,d,e)=

(a) (1,1000,1,1000,1)

(b) (1,1,1,1,1)

(c) (1,2000,1,2000,1)

(d) (1,0,1,0,1)

21. The initial value problem x dy/dx = y + x², x > 0, y (0) = 0 has

(a) No solution

(b) Infinitely many solutions

(c) Unique solution

(d) Exactly two solutions.