Reference no: EM131107264

Honors Exam 2010 COMBINATORICS

1. Patrol officers are to be paired for the 3-11 pm shift. Each pair must have an experienced and an inexperienced officer who are compatible. Compatible pairs are indicated below.

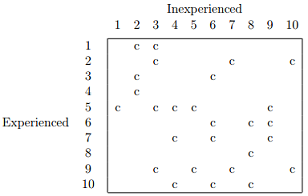
(a) What is the largest possible number of pairs with each officer in at most one pair?

(b) Prove that your answer to (a) is correct. Your proof should, of course, be concise.

(c) If the compatibility table was replaced by a ratings matrix C with nonnegative real entries and the goal was to maximize the sum of the ratings of the formed pairs, why is there a best pairing among the optimal solutions to the following problem?

Maximize ∑_i,j c_ijx_ij

subject to ∑_jx_ij = 1, for i = 1, . . . , 10

                    ∑_ix_ij = 1, for j = 1, . . . , 10

                   x_ij ≥ 0, for all (i, j).

2. A non-increasing sequence λ = (λ₁, λ₂, . . .) of nonnegative integers whose sum |λ| is finite is called a partition of n if |λ| = n. We call λ_i a part of λ if λ_i > 0. Prove the following facts. At least one of your proofs should use a generating function and at least one should use a bijection.

(a) The number of partitions of n into distinct parts equals the number into odd parts.

(b) The number of partitions of n into odd parts of which exactly k are distinct equals the number into distinct parts in which exactly k sequences of consecutive positive integers occur. (For example, (11, 11, 9, 5, 5, 5, 0, . . .) has exactly 3 distinct odd parts and in (11, 10, 9, 8, 6, 2, 0, . . .) exactly 3 sequences of consecutive positive integers occur.)

 (c) The number of partitions of n into distinct parts such that ∑_i≥1(-1)^i-1λ_i = k equals the number into k odd parts.

3. Let n ≥ 0 be an integer, and let [n] = {1, 2, . . . , n} (so that [0] = ∅). A set partition of [n] is a collection of nonempty disjoint subsets of [n], called blocks, whose union is [n]. The number of set partitions of [n] is called the n^th Bell number b_n. The number of blocks in a set partition π is denoted |π|. The n^th Bell polynomial is the polynomial b_n(q) = ∑_πq|π|, where the sum is over set partitions π of [n] (so that b_n(1) = b_n). For example, b₄ = 15 and b₄(q) = q + 7q² + 6q³ + q⁴.

(a) Find ∑_n≥0b_n(xⁿ/n!).

(b) Prove that the sequence of Bell numbers is log-convex: b_n² ≤ b_n-1b_n+1 for n ≥ 1. Does the fact that b_kb_l ≤ b_k-1b_l+1 for k ≤ l follow?

(c) Prove that the sequence of Bell polynomials is q-log-convex: b_n-1(q)b_n+1(q) - b_n(q)² has nonnegative coefficients for n ≥ 1. Does the fact that b_k-1(q)b_l+1(q) - b_k(q)b_l(q) has nonnegative coefficients for k ≤ l follow?

4. Let τ, µ and ν be partitions such that |τ | = |µ| + |ν|. Let f(τ, µ, ν) be the number of functions T with domain {(i, j)| µ_i < j ≤ τ_i} such that the number of pairs (i, j) that T maps to k is ν_k, for k ≥ 1, and such that

• T(i, j) ≤ T(i, j') for j < j';
• T(i, j) < T(I', j) for i < I';
• n_k(I, J) ≥ n_k+1(I, J) for I ≥ 1, µ_I ≤ J < τ_I and k ≥ 1,

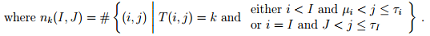
(a) What is the algebraic significance of the numbers f(τ, µ, ν)?

(b) Why does f(τ, ν, µ) equal f(τ, µ, ν)?

(c) What is f(τ, µ, ν) if µ = (0, 0, . . .) and ν = (1, . . . , 1, 0, . . .)?