Reference no: EM131391

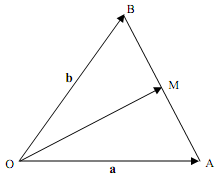
Question 1. OAB is an isosceles triangle with OA = OB and M is the mid-point of AB. Let OA' = a and let OB' = b.

(a) Write the vectors AB' and OM' as linear combinations of the vectors a and b.

(b) Use vector methods to show that OM' is perpendicular to AB'.

Question 2. Let u = (1, 3, 2), v = (3,1, 2) and w = (4,0,1) be three vectors in R³. Find the subsequent.

(a) 3u - 2v + 4w 

(b) u.w

(c) v x w

(d) proj_vu

(e) cosine of the angle between the vectors u and v.

Question 3. Show that the 3 points P = (1, 3, 4), Q = (3, 2, 5) and R = (5, 1, 6) all lie on the same straight line.

Question 4. Let u = (3, 1, 0) and v = (1, 2, c) be two vectors in R³. For what value(s) of c is the angle between the vectors equal to 60°?

Question 5. Let u = (8, 12, 1) and v = (4, 6, k) be two vectors in R³.

(a) For what value(s) of k will the two vectors u and v be parallel? Explain.

(b) For what value(s) of k will the two vectors u and v be orthogonal? Explain.

(c) For what value(s) of k will the two vectors u and v be of equal length?

Question 6. Let l: 2x + 5y = 9 be a line and P = (3, 6) be a point in R².

(a) Let Q be the point on the line l having its y-coordinate = 0 and let R be the point on the line l having its x-coordinate = 0. Find the coordinates of the points Q and R.

(b) Plot the points P, Q, R and the line l on a two-dimensional Cartesian coordinate system.

(c) Find the components of the vector QP'.

(d) Find a normal vector n to the given line l.

(e) Find the distance between the point P and the line l. 

Question 7. The plane x + 2y+  2z = intersects the positive coordinate axis OX, OY and OZ in three points A, B and C respectively.

(a) Find the coordinates of the three points A, B and C.

(b) Find the area of the triangle ABC.