Solve system by applying gauss-jordan elimination

Reference no: EM133348716

Question 1. Use the determinant to find all values α ∈ C such that the matrix

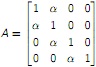
is invertible.

Question 2. Let A ∈ F^m×nand let b ∈ F^m×1. Prove that the linear system Ax = 0 has a nonzero solution x ∈ F^n×1 if and only if the n columns of A are linearly dependent.

Question 3. Consider the three linear systems of equations:

x₁ + x₂ = -7 x₁ + x₂ = 2 x₁ + x₂ = 2
x₂ + 2x₃ = 10 x₂ + 2x₃ = 3 x₂ + 2x₃ = 4
2x₂+ x₃ = 2 2x₂ + x₃ = 3 2x₂ + x₃ = -1

corresponding to the systems Ax = b, Ax = c, and Ax = d respectively. Solve all three systems simultaneously by applying Gauss-Jordan elimination to the 3 × 6 augmented matrix [A | b c d ].

Question 4. Consider the linear system of equations:

x₁ - αx₂ = 3
x₂ - βx₃ = 0
-γx₁ + x₃= -2

Find conditions on α, β, γ ∈ R such that the system has no solutions, a unique solution, and infinitely many solutions. In the latter two cases, find the solution set. (Note. Your solution(s) may be in terms of α, β, and γ.)

Reference no: EM133348716

Questions Cloud

What key factors accounted for the outcome of the elections : Analyze the recently concluded Mid-term elections. What key factors accounted for the outcome of the elections? List and explain these key factors.

What roles do they play in a representative democracy : Why do we have political parties? What roles do they play in a representative democracy? How can these roles be beneficial? How can they be harmful?

Determinism from personal perspective : According to determinism from a personal perspective. human behavior is not determined by current and historical environmental events.

What is occupational primary responsibility : What is an occupational therapist? What is an occupational primary responsibility? What credentials does an occupational therapist hold?

Solve system by applying gauss-jordan elimination : Solve all three systems simultaneously by applying Gauss-Jordan elimination to the 3 × 6 augmented matrix [A | b c d ].

Explain the problem of climate change : Explain the problem of climate change and why is this a global problem? and pick a developed and a developing state and compare their response

How can land use planning be used to combat obesity : How can land use planning be used to combat obesity? How would the success of the implementation work or isn't working? Consider each intervention's federal

Explain impact of gender-cultural values and dimensions : Explain the impact of gender, cultural values and dimensions, and group dynamics in the scenario.

Why should a country socio-economic diversity : Should a country's socio-economic diversity or geographic size should factor into the development of its governmental system? In other words

User Account

All Pages