Reference no: EM132291009

Design and Analysis of Algorithms Assignment Questions -

Q1. Consider the AVL-tree T as shown in Fig. 1 below, where the numbers are the keys stored.

(a) Copy the tree in your write-up, and for each node v label the height of the subtree rooted at v. (We define the height of a null node to be 0 and the height of a leaf to be 1). Verify that this is indeed a valid AVL-tree.

(b) Suppose now we insert a key 19 to the tree T, and then insert another key 4 to T. For each insertion, show the resulting tree right after the insertion (i.e., before any re-balancing), and the tree after each structural change during re-balancing, as well as the final tree.

(c) Ignoring the insertions in part (b), suppose we delete the key 14 from the tree T as shown in the figure. We use the policy that when an internal node with no null child is deleted, we replace the deleted key with its successor key in the tree whenever the successor key is available. Show the tree right after the deletion (i.e., before any re-balancing), and the tree after each structural change during re-balancing, as well as the final tree.

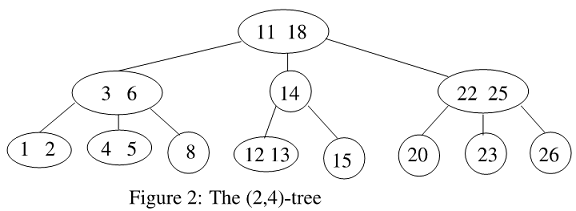
Q2. Show the results of deleting keys 18, 15, 13, in that order, from the (2, 4)-tree shown in Fig. 2 below (where the numbers shown are the keys stored), using the one-pass top-down deletion algorithm of B-trees as discussed in class and described in the Textbook pages 500-502.) Note that for both the transfer and the fusion operations in Step 3a and Step 3b, if the immediate left and right sib-lings are both available for the operation, we use the policy of always using the left sibling. For each deletion, show the tree after each structural change and the final tree, and also state the case number being applied.

Attachment:- Assignment File.rar