Reference no: EM131081251

Sample midterm 2 questions-

1. Let (f_n) be a sequence of uniformly continuous functions on an interval (a, b), and suppose that fn converges uniformly to a function f. Prove that f is uniformly continous on (a, b).

2. Prove that the functions

d₁(x, y) = (x - y)⁴, d₂(x, y) = 1 + |x - y|,.

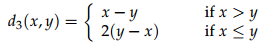
are not metrics on R.

3. Find the radius of convergence of the series

_n=0∑^∞xⁿ/n^√n,        _n=0∑^∞4ⁿx²ⁿ⁺¹,       _n=0∑^∞x^{n^2}.

4. Suppose that f_n converges uniformly to f on a set S ⊆ R, and that g is a bounded function on S. Prove that the multiplication g · f_n converges uniformly to g · f.

5. Let (f_n) be a sequence of bounded functions on a set S, and suppose that fn → f uniformly on S. Prove that f is a bounded function on S.

6. Let (f_n) be a sequence of real-valued continuous functions defined on the interval [0, 1]. Suppose that f_n converges uniformly to a function f. Define a global bound M according to

M = sup{|f_n(x)|: n ∈ N, x ∈ [0, 1]}.

Prove that M is finite.

7. (a) Prove that the function

d(x, y) = min{|x - y|, 1}

is a metric on R.

(b) Is the set (-5, 5) open with respect to this metric? Prove your assertion.

8. (a) Find the radius of convergence of the power series

f₁(x) = _n=1∑^∞xⁿ/n²,            f₂(x) = n=0∑∞ x²ⁿ/2ⁿ.

(b) Show that the series

f₃(y) = _n=1∑^∞(1/n²)(y/1 + y²)ⁿ

converges for all values of y ∈ R.

9. Consider the function defined on the domain [0, ∞) as

Define a sequence of functions on the interval [0, 1] according to f_n(x) = g(nx).

(a) What is the maximum value of g(x), and where is it attained?

(b) Sketch the functions f₁(x), f₂(x), and f₃(x) on [0, 1].

(c) Prove that f_n converges point-wise to a function f on [0, 1], and determine f.

(d) Does f_n converge uniformly to f on [0, 1]? Prove your assertion.

10. Let (f_n) be a sequence of continuous functions on [a, b] that converges uniformly to f on [a, b]. Show that if (x_n) is a sequence in [a, b] and if x_n → x, then limn→∞ f_n(x_n) = f(x).