Reference no: EM132318403

Mathematical Analysis Assignment Questions -

Question 1 -

a) Let f : [a, b] → R be continuous. Prove that f is bounded.

b) State (but do not prove) the Mean Value Theorem. Deduce that if f is differentiable on R with derivative 0 then f is constant.

c) Let c: R → R be a twice differentiable function satisfying

c''(x) = -c(x), for all x

and c(0) = 1, c'(0) = 0.

Let f (x) = c'(x) cos x + c(x) sin x for x ∈ R.

Show that f(x) = 0 for all real x.

d) With c as in the previous part consider the function u given by

u(x) = c(x)/cos x, for - π/2 < x < π/2

and show that c(x) = cos x for - π/2 < x < π/2.

Question 2 -

a) Show that the maximum value of (1 - x)e^x on the real line is 1.

b) State (but do not prove) 1'Hopital's rule for computing the limit of a ratio of two differentiable functions

lim_x→c f(x)/g(x).

c) Consider the function f defined by

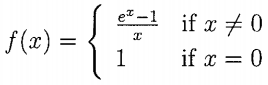
(i) Prove that f is differentiable at 0 and find its derivative there.

(ii) Show that f' is non-negative at all points other than 0.

Question 3 -

a) Assuming that log t ≤ t - 1 for all t > 0 show that

log t ≥ 1 - 1/t

for all t > 0.

b) Deduce that for all t > 0

t log t ≥ t - 1.

c) Let p₁, p₂, . . . , p_m be positive numbers with ₁∑^mp_i =1.

Show that

₁∑^mp_ilog(mp_i) ≥ 0.

d) With p₁, p₂, . . . , p_m as before show that

₁∑^mp_ilogp_i ≥ -logm.

e) Find positive numbers p₁, p₂, . . . , p_m adding up to 1 for which

₁∑^mp_ilogp_i = -log m.

Question 4 -

a) Taylor's Theorem with Lagrange remainder states that if f is n-times differentiable on an open interval containing a and x then

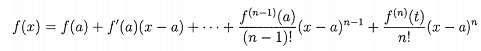
for some t between a and x.

Use this with n = 3 and a = 0 to approximate e^x by its quadratic Taylor approximation arid find an expression for the error.

b) Show that if x ≥ 0 then e^x ≥ 1 + x + x²/2 but if x < 0 then e^x < 1 + x + x²/2.

c) Show that for any x

e^x ≤ 1 + x + x²/2 + x³e^x/6.

d) Deduce that if x < 6^1/3

e^x ≤ (1 + x + x²/2)/(1 - x³/6).

e) Expand

1/(1 - x³/6)

as a power series centred at 0 and use this to calculate the first 5 terms of the power series for

(1+ x + x²/2)/(1 - x³/6).

Attachment:- Assignment File.rar