Reference no: EM13838435

Problem 1: The mean of the Standard Normal Distribution is.

Problem 2: In a Normal distribution, percent of the data falls below the mean.

Problem 3: Consider the following data: 30, 30, 33, 35, 37, 40, 40, 43, 45, 50. What is its five number summary?

Problem 4: The amount of time (in minutes) that students at a particular school need to complete a standardized test follows the N(40, 6) distribution.

a) If students are given 45 minutes to complete the exam, draw an appropriate picture (with shading) that represents the amount (percent/proportion) of students expected to finish in the allotted time.

b) If students are given 45 minutes to complete the exam, what percent of students would be expected to finish in the allotted time?

c) How much time would need to be allotted so that 90% of the students would be able to finish the exam.

Problem5: Suppose the scores on a particular test have a Normal distribution with mean 60 and standard deviation 15.

a) Approximately 68% of the scores fall between and .

b) Approximately percent of the test-takers received a score of at least 75.

c) Bobby took the exam and received a score of 87. His score was standard deviations above the mean.

d) There are 36 students in the class, and we take a sample of 16 of them, of which 3 have blue eyes. What is the probability that the average score of our sample is above 87?

Problem 6: A simple random sample of size 5 is chosen from the 26 letters of the alphabet. Which of the following
statements are true?

a) It is impossible to randomly choose the letters A, B, C, D, E.

b) It is impossible to randomly choose the letters A, E, I, O, U.

c) It is possible to randomly choose the letters A, B, C, D, E but choosing the set R, D, K, E, J is more likely.

d) Both (a) and (b) are true.

e) None of the above.

Problem 7: Which of the following are valid probability distributions for a weighted 6-sided dice? (Select all that apply)

Outcome	A	B	C	D
1	½	½	1	1/6
2	¼	½	1	1/6
3	1/8	1/3	1	1/6
4	1/16	-1/3	1	2/6
5	1/16	¼	0	0
6	0	-1/4	0	0

Problem 8: An experiment is performed in which the outcomes follow a N(500, 12) distributions. This experiment is repeated a fixed number of times and the mean ¯x is recorded. How many times must the experiment be repeated so that the standard deviation of ¯x is 3?

a) 4
b) 2
c) 16
d) 3

Problem 9: The critical z∗ value for constructing a 92% confidence interval for a population µ is closest to

a) 1.76
b) 1.41
c) 0.82
d) 2.05
e) 1.75

Problem 10: The critical t∗ value for constructing a 92% confidence interval for a population µ from a sample of 30 subjects is closest to

a) 1.31
b) 0.82
c) 1.41
d) 1.81
e) 2.05

Q 11: Suppose the heights of American women are approximately normal. Nine women were chosen at random and their heights recorded:

60.25 62.75 58.50
67.50 63.50 62.75
65.25 64.75 60.00

The median of these numbers is 62.75, the mode is 62.75, the average is 62.81, and the standard deviation is 2.86. Between what two numbers can we say that we are 92% sure that the average height of American women lies between? (Show your workings)

Problem 12: The mean area µ of the several thousand apartments in a new development by a certain builder is advertised
to be 1300 ft². A tenant group thinks this is inaccurate, and suspects the average is actually less than1300 ft². Apartments are randomly selected and carefully measured. The appropriate null and alternative hypotheses relevant to this is example are

a) H0 : µ = 1300 and Ha : µ < 1300
b) H0 : µ = 1300 and Ha : µ > 1300
c) H0 : µ = 1300 and Ha : µ 6= 1300
d) Unable to determine without knowing the sample size.

Problem 13: Fill in all the blanks below.

A snack food producer produces bags of peanuts that are labeled as containing 4 ounces of peanuts. As part of quality control, for every 10,000 bags produced, we select 35 bags at random and weigh their contents. Assume that the average weight for the whole batch is 4 ounces. What is the probability that when we randomly select 35 bags that their average weight is at least 4.54 ounces with standard deviation 5 ounces?

a) In order to establish this we first calculate the test statistic given by

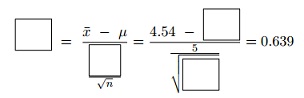
b) The reason we calculated this test statistic is because the area to the right of 4.54 on the curve N (4, 5/√35) is now equal to the area to the right of___________ on the curve t(34).

 

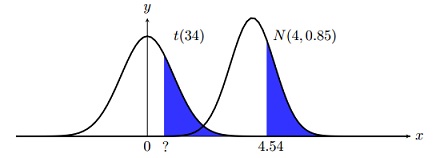
c) We take this test statistic value and go to Table (the normal distribution table is Table A, the t distribution table is Table C). From this table we find that the area to the right of 4.54 on the curve N (4, 5/√35)is at least _____% of the total area under N (4, 5/√35).

d) Knowing this P-value means (select one):

(i) If the average weight of the batch is 4 ounces, then there is, at least, a 25% chance that a sample of 35 bags will have average weight 4.54 ounces or more.

(ii) If the average weight of the batch is 4 ounces, then there is, at least, a 75% chance that a sample of 35 bags will have average weight 4.54 ounces or more.

(iii) The probability that a sample of 35 bags weighs more than 4.54 ounces is 0.639.

(iv) None of the above.