Reference no: EM131279388

Project:1. Project Overview

In this project, you are asked to implement Graham's scan and Javis' march to construct the convex hull of an input set of points in the plane, and compare their execution times. For a description of the algorithm, please refer to the lecture notes "convex-hull.pptx" on Wednesday Oct 26th.

We make the following two assumptions:

a) All the input points have integral coordinates ranging between -50 and 50.
b) The input points may have duplicates.

In a), integral coordinates are assumed to avoid issues with floating-point arithmetic. The rectangular range [-50, 50] × [-50, 50] is big enough to contain 10,201 points with integral coordinates. Since the input points will be either generated as pseudo-random points or read from an input file, duplicates may appear.

The classes PureStack and ArrayBasedStack should not be modified. Four classes from Project 2 will be modified or reused for this project: Segment, Plot, Point, and PolarAngleComparator,. No need to modify Segment and Plot.

Modify your implementation of the class Point so that the compareTo() method now compares y-coordinate first. The class PolarAngleComparator has an additional instance variable flag used for breaking a tie between two points which have the same polar angle with respect to the reference point (stored in the instance variable referencePoint). When flag == true, the point closer to referencePoint is considered smaller; when flag == false, the further point is considered smaller.

2. ConvexHull Class

Convex hull construction is implemented by the abstract class ConvexHull, which has two constructors:

public ConvexHull(Point[] pts) throws IllegalArgumentException

public ConvexHull(String inputFileName) throws FileNotFoundException,

InputMismatchException

The first constructor takes an array pts[] of points and copy them over to the array points[]. The array pts[] may consist of random points, or more precisely, points whose coordinates are pseudo-random numbers within the range [-50, 50] × [-50, 50]. After Project 2, you are assumed to be familiar with random point generation. (Just in case not, please read Section 5.)

The second constructor reads points from an input file of integers. Every pair of integers represents the ?? and ??-coordinates of a point. A FileNotFoundException will be thrown if no file with the inputFileName exists, and an InputMismathException will be thrown if the file consists of an odd number of integers. (There is no need to check if the input file contains unneeded characters like letters since they can be taken care of by the hasNextInt() and nextInt() methods of a Scanner object.)

For example, suppose a file points.txt has the following content (this was the same example file used in the description of Project 2):

0 0 -3 -9 0 -10
8 4 3 3
-6 3
-2 1
10 5
-7 -10
5 -2
7 3 10 5
-7 -10 0 8
-1 -6
-10 0
5 5

There are 34 integers in the file. A constructor call ConvexHull("points.txt") will initialize the array points[] to store 17 points below (aligned with five points per row just for display clarity here):

(0, 0)	(-3, -9)	(0, -10)	(8, 4)	(3, 3)
(-6, 3)	(-2, 1)	(10, 5)	(-7, -10)	(5, -2)
(7, 3)	(10, 5)	(-7, -10)	(0, 8)	(-1, -6)
(-10, 0)	(5, 5)

Note that the points (-7, -10) and (10, 5) each appear twice in the input, and thus their second appearances are duplicates. The 15 distinct points are plotted in Fig.1 by Mathematica.

There is a non-negligible chance that duplicates occur among the input points, whether they are from the input file or randomly generated from the range [-50, 50] × [-50, 50]. For a fair comparison between Graham's scan and Javis' march, both assuming their input points to be distinct, all the duplicates should be eliminated before the convex hull construction. This is done by the constructors via calling the method removeDuplicates().

The method removeDuplicates() performs quicksort on all the points by y-coordinate. After the sorting, equal points will appear next to each other in points[]. The method creates an object of the class QuickSortPoints to carry out quicksort using a provided Comparator<Point> object, which invokes the compareTo() method in the class Point. After

the sorting, identical points will appear together, and duplicates will be easily removed. Distinct points are then saved to the array pointsNoDuplicate[] with the element at index 0 assigned to lowestPoint.

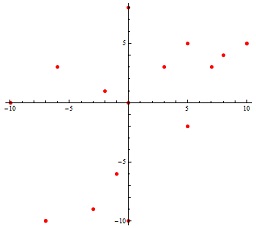
Fig. 1. Input set of 15 different points.

In the previous example, quicksort produces the following sequence:

(-7, -10)	(-7, -10)	(0, -10)	(-3, -9)	(-1, -6)
(5, -2)	(-10, 0)	(0, 0)	(-2, 1)	(-6, 3)
(3, 3)	(7, 3)	(8, 4)	(5, 5)	(10,5)
(10, 5)	(0, 8)

The two (-7, -10)s appear together, so do the two (10, 5)s. After removal of duplicates,
the remaining points are copied over to the array pointsNoDuplicate[]:

(-7, -10)	(0, -10)	(-3, -9)	(-1, -6)	(5,-2)
(-10, 0)	(0, 0)	(-2, 1)	(-6, 3)	(3,3)
(7, 3)	(8, 4)	(5, 5)	(10, 5)	(0,8)

The variable lowestPoint is set to (-7, -10).

The array pointsNoDuplicate[] will be the input of a convex hull algorithm. The class ConvexHull has an abstract method constructHull() which will be implemented by its subclasses to carry out convex hull construction using either Graham's scan or Jarvis' march.

public abstract void constructHull();

The vertices of the constructed convex hull will be stored in the array hullVertices[] in counterclockwise order starting with lowestPoint.

2. Convex Hull Construction

Two algorithms, Graham's scan and Jarvis' march, are respectively implemented by the subclasses GrahamScan and JarvisMarch of the abstract class ConvexHull. Both subclasses must handle the special case of one or two points only in the array pointsNoDuplicates[], where the corresponding convex hull is the sole point or the segment connecting the two points.

Graham's scan

The class GrahamScan sorts all the points in points[] by polar angle with respect to lowestPoint. Point comparison is done using a Comparator<Point> object generated by the constructor call PolarAngleComparator(lowestPoint, true). The second argument true ensures that points with the same polar angle are ordered in increasing distance. (In case your previous implementation did not work well, this is a chance to make it up. ) The compare() method must be implemented using cross and dot products not any trigonometric or square root functions. (Please read the Javadoc for the compare() method carefully.)

Point sorting above is carried out by quicksort as follows. Create an object of the QuickSortPoint class and have it call the quicksort() method using the PolarAngleComparator object mentioned in the above paragraph. The comparator uses lowestPoint as the reference point. Note that quicksort has the expected running time O(n log n) and the worst-case running time O(n² ), which will respectively be the expected and worst-case running times for this implementation of Graham's scan for convex hull construction.

Sorting is performed within the method setUpScan(). In the array pointsNoDuplicate[], (- 1, -6) and (5, -2) have the same polar angle with respect to (-7, -10). That (-1, -6) appears before (5, -2) is because it is closer to (-7, -10).

Graham's scan is performed within the method constructHull() on the array pointsNoDuplicate[] using a private stack vertexStack. As the scan terminates, the vertices of the constructed convex hull are on vertexStack. Pop them out one by one and store them in a new array hullVertices[], starting at the highest index. When the stack becomes empty, the elements in the array, in increasing index, are the hull vertices in counterclockwise order.

Jarvis' March

This algorithm of the gift wrapping style is implemented in the class JarvisMarch. There are three private instance variables.

private Point highestPoint; private PureStack<Point> leftChain;
private PureStack<Point> rightChain;

The algorithm builds the right chain from lowerestPoint to highestPoint and then the left chain from highestPoint downward to lowestPoint. Two stacks, leftChain and rightChain, are used respectively to store the chains during the construction. The convex hull vertices on the stacks are later merged into the array hullVertices[].

The convex hull construction is described with more details in the PowerPoint notes "convex hull.pptx". At each step, the method

private Point nextVertex(Point v)

determines, given the current vertex v, the next vertex to be the point which has the smallest polar angle with respect to v. In the situation where multiple points attain the smallest polar angle, the one that is the furthest from v is the next vertex. Hence, the comparator used in this construction step should be generated by the call PolarAngleCompartor(v, false).

3. Display the Convex Hull

The constructed convex hull will be displayed again using Java graphics package Swing. Please refer to Section 4 in the description of Project 2 for a brief introduction to Swing. The outputs by the two convex hull algorithms are displayed in separate windows. For display, a separate thread is created inside the method myFrame() in the class Plot. Please do not modify this class for better display unless you understand what is going on there.

The class Segments has been implemented for creating specific line segments to connect the input points so you can see the correctness of the sorting result.

The output of each algorithm can be displayed by calling the partially implemented method draw() in the ConvexHull class, only after constructHull() is called, via the statement below:

Plot.myFrame(pointsNoDuplicate, segments, getClass().getName());

where the first two parameters have types Point[] and Segment[], respectively. The call getClass().getName() simply returns the name of the convex hull algorithm used. From hullVertices[] you will generate the edges of the convex hull as line segments and store them in the array segments[]. This can be done by iterating through the element in the array in one loop. Do not forget to generate a segment connecting the last element with the first point at index 0, that is, lowestPoint.

For the example in Section 1, the array Segment[] contains 5 segments below (where each element is shown as a pair of points):

((-7, -10), (0, -10))
((0, -10), (10, 5))
((10, 5), (0, 8))
((0, 8), (-10, 0))
((-10, 0), (-7, -10))

Fig. 1 displays the convex hull constructed over pointsNoDuplicate[] for the same earlier example.

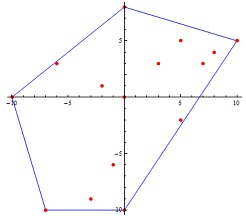
Fig. 2. Convex hull of the input points shown in Fig. 1.

4. Compare Convex Hull Algorithms

The class CompareHullAlgorithms executes Graham's scan and Jarvis' march on points randomly generated or read from files. If the input points are not from an existing file, , its main() method calls the method generateRandomPoints() to supply an array of random points Over each input set of points, the method compares the execution times of these algorithms in multiple rounds. Each round proceeds as follows:

a) Create an array of randomly generated integers, if needed.

b) For each of GrahamScan and JavisMarch, create an object from the above array or an input file.

c) Have the two created objects call the construcHull() method and store the results in
hullVertices[].

Below is a sample execution sequence with running times. Use the stats() method to create a row for each sorting algorithm in the table.

Comparison between Convex Hull Algorithms

Trial 1: 1
Enter number of random points: 1000

algorithm size time (ns)
---------------------------------------
Graham's Scan 1000 884260
Jarvis' March 1000 1096228
---------------------------------------

Trial 1: 2
Enter number of random points: 500

algorithm size time (ns)
---------------------------------------
Graham's Scan 500 524578
Jarvis' March 500 791930
---------------------------------------

Trial 3: 2
Points from a file File name: points.txt

algorithm size time (ns)
---------------------------------------
Graham's Scan 17 23955
Jarvis' March 17 12991
---------------------------------------

5. Random Point Generation

To test your code, you may generate random points within the range [-50, 50] × [-50, 50]. Such a point has its ??- and ??-coordinates generated separately as pseudo-random numbers within the range [-50, 50]. You already had experience with random number generation from Project 1. Import the Java package java.util.Random. Next, declare and initiate a Random object like below

Random generator = new Random(); Then, the expression generator.nextInt(101) - 50

will generate a pseudo-random number between -50 and 50 every time it is executed.

Attachment:- template.zip