Reference no: EM131679666
Topics In Discrete Mathematics
PART I -
1. Name and define the four components of Mathematical system.
2. Name and define the three types of reasoning.
3. Name and define the four characteristics of a good definition.
4. Define the following terms:
a. Statement
b. Set
c. Subset
d. Venn Diagram
e. Union
f. Tautology
g. Contradiction
h. Mathematical induction
i. Hypothesis
j. Function
k. Relation
l. Logic
m. Law of Detachment
PART II - ANSWER 15 QUESTIONS.
NOTE: YOU MUST SHOW ALL YOUR WORK.
1. Give the converse, Inverse and contrapositive for each of the following propositions.
a. (q∨ r) ? P
b. If x + y is odd and y + z is odd, then x + z is odd.
2. Consider the proposition p(n)="n2+5n+1 is even".
a. Prove that p(k)→p(k +1)for all k in P.
b. For which values of n is p(n) actually true? What is the moral of this exercise?
3. Prove or disprove
a. Let m, n, dbe integers, if 3 divides the sum m and n of positive integer m and n, then 3|m or 3|n.
b. Let m, n, and d be integers. Show that if d|m, and d|n then d|m(m + n
4. For the following relations on S = {0, 1, 2, 3}, specify which of the properties (R), (AR), (S), (AS) and (T)
a. (m, n) ∈ R1 if m - n = 2
b. (m, n) ∈ R2 if m + n is even
c. (m, n) ∈ R3 if m ≤ n
d. (m, n) ∈ R4 if m + n ≤ 4
5. f = {(1, a), (2, b), (3, c), (4, d)} be a function from X = {1, 2, 3, 4}, to Y = {a, b, c, d}. Let S = {3, 4}, W = {a, d}, and V = {b, d}. Find
a. ff-1
b. f(S)
c. f-1(W), and
d. f(f-1(V))
6. Suppose that P, Q and R are statements. Complete the following truth table.
|
P
|
Q
|
R
|
Q ∨ R
|
~Q
|
P Λ ~Q
|
P ⇒ (Q ∨ R)
|
(P Λ ~Q) ⇒ R
|
|
T
|
|
T
|
|
F
|
|
|
|
|
T
|
T
|
F
|
|
|
|
|
|
|
F
|
T
|
|
T
|
T
|
|
|
|
T
|
|
|
F
|
T
|
|
|
|
|
F
|
T
|
T
|
|
|
|
|
|
|
|
F
|
T
|
F
|
F
|
|
|
|
F
|
F
|
|
T
|
|
|
|
|
|
F
|
|
F
|
F
|
T
|
|
|
|
ii. Identify the last column
7. While searchingfor the cause of a mysterious disease which has stricken 200 people, researchers have focused their attention on three activities occurring in a certain hotel. They have surveyed the 180 victims to determine how many attended a lunch, a banquet, or a party given there. Unfortunately, one page of the survey results has been destroyed.
Only the following information remains
- 16 people attended the lunch, the banquet, and the party
- 20 people had nothing to do with the hotel
- 24 people attended the party and the lunch.
- 32 people attended the lunch and the banquet.
- 28 people attended the banquet and the party
- 80 people attended the lunch.
- 28 people attended the banquet but had no other contact with the hotel.
Organize the information into mutually exclusive categories.
a. Draw the Venn diagram of this report.
b. Complete the following table below for your analysis:
ACTIVITIES SYMBOLS NUMBER OF ATTENDANTS
Lunch only L
Banquet only B
Party only P
Lunch and Banquet only L & B
Lunch and Party only L & P
Banquet and Party only B & P
Lunch and Banquet and Party A & B & P
None of Lunch, Banquet, or Party None
TOTAL
8. Let f: R ? R be given byf(x) = x^2. Find the following.
a. f-1 (|4|)
b. f-1 (9)
c. f -1 ([1, 4])
9. Prove or disprove
a. The sum of two consecutive odd integers is an even integer.
b. That n2 - 2 is not divisible by 5 for any positive integer n
c. The product of an odd integer and an odd integer is even
10. Determine whether each of the following argument is Valid.
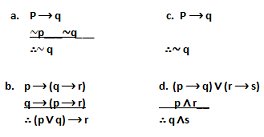
11. Let P (n) be the propositional function "x3 ≥ x2" Tell whether each of the following proposition is true or false. The domain of discourse is R.
a. P(1) c. P(2)
b. P (1/2) d. ∀xP(x)
e. ∃x P(x) f. ∼(∀x P(x)
12. Consider the following pair of sets:
A = {x2 - 3x + 2 = 0}, B = {x3 - 6x2 +11x - 6 = 0}, C = {x4 -10x3 + 35x2 - 50x + 24 = 0}
Find
a. A ∪ B ∪ C
b. A ∩ B∩ C
c. (A ∪ B ∪ C)c
d. Draw the Venn diagram for a, b and c above.
e. How many subsets can be formed from set C?
f. What is the power set of A ∩ B ∩ C.
g. What is the cardinality of A ∩ B ∩ C.
h. Find C - A.
Q13. With apologies to Sidney Harris for trading on his terrific cartoon (shown below). I'd like to play a little with the dog's statement. Consider the assertions made by the dog:
A: = "All cats have four legs"
B: = "I have four legs"
C: = "I am a cat"
(Are these assertions statements or predicates? Explain.) The dog's statement is of the form "If A and B, then C".
a. Construct a truth table for the statement "If A and B, then C"
Q14. (a) Let a, b ∈ R, with a ≠ 0. Show that f: R →R, given by f(x) = ax + b is a one-to-one correspondence. (What happens if a = 0?)
(b) Show that for all positive real numbers k, f: (-k2, ∞) → (-∞, k), given by f(x) = kx/(x + k2) is a one-to-one correspondence.
(c) Show that there exists no positive real number k for which f: R → R, given by f(x) = √(kx2+5) is a one-to-one correspondence.
15. These example suggest a general strategy for finding gcd(m, n): Replace m and n by n and m MOD n and try again.
AlgorithmGCD(integer, integer)
{Input: m, n ∈ N, not both 0.}
{Output: gcd(m, n).}
{Auxiliary variable: integers a and b.}
a := m; b := n
{The pairs (a, b) and (m, n) have the same gcd.}
While b ≠ 0 do
(a, b) := (b, a MOD b)
return a
Use the above to determine the following: m = 45, n = 12
16. We define f: R → R as follows:
{ -x3 if x < 0
f(x)={ x3 if x ≥ 1
{ x if 0 ≤ x < 1
a. Calculate f(3), f(1/3), f(-1/3), and f(-3).
b. Sketch a graph of f.
c. Find lm(f).
17. What are the quotient and remainder when
a. 44 is divided by 8?
b. -123 is divided by 19?
c. 0 is divided by 17?
d. 1,234,567 is divided by 101
18. How many positive integers between 5 and 31
a. Are divisible by 3? Which integers are these?
b. Are divisible by 4? Which integers are these?
c. Are divisible by 3 and by 4? Which integers are these?
19. Determine the following:
a. How many bit strings are there of length eight?
b. How many bit strings are there of length six or less, not counting the empty string?
20. a. Build a digital circuit that produces the output (p V ¬ r) ^ (p v (¬q v r)) when given input bits p, q, and r.
b. Construct a combinatorial circuit using inventers, OR gates and AND gates that producesthe output ((¬p v ¬q) ^ (¬p v ( q ^ r) ) from input bits p, q, and r.
Need part 2 only.