Reference no: EM131567359
Assignment: Congruent Triangles
1. Given: Δ ABC ≅ Δ DEF
Draw the triangles in the space provided below and label the vertices. List the sets of corresponding angles and the corresponding sides (there should be 3 pairs for each).
Corresponding Angles Corresponding Sides
2. For this activity, you will need two plastic straws. If you do not have straws available, you can also use dry spaghetti noodles, pipe cleaners, or string. Complete parts A-H to obtain full credit.
A. Take one straw and cut it into three pieces of any length. Always be careful to maintain proper techniques when using scissors.

B. Take the second straw and cut it into three pieces; these three pieces should be the same length as the three pieces of the first straw. Use your pieces from Part A as a guide to cut the second straw.

C. Make a triangle using the straw pieces from Part A.
D. Make a triangle using the straw pieces from Part B.
E. Set your triangles on the paper in the space provided below and trace them. If you have access to a camera, you may also take pictures of your triangles and insert them into the document.
|
Triangle #1 (Part A)
|
Triangle #2 (Part B)
|
|
|
|
The following questions (F-H) will be answered on the chart below. These questions should be answered using 2-4 complete sentences with proper grammar and punctuation.
F. How do your triangles compare to each other?
G. Can you make your triangles look different from one another?
H. Which postulate (from lessons 4 or 5) does this activity prove? Explain.
3. State the postulate or theorem that you would use to prove each pair of triangles congruent. State all of the pairs of congruent parts you are using.
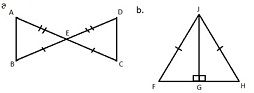
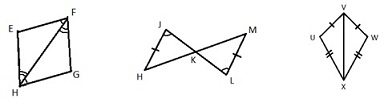
4. Explain how you can use SSS, SAS, ASA, or AAS along with CPCTC to prove each statement true. Remember: For these problems, you must first prove that the two triangles are congruent, and then you can use CPCTC to show that the parts are congruent.
a. Prove HE‾ ≅ FG‾ b. Prove JK‾ ≅ KL‾ c. Prove ∠U ≅ ∠W
|
Find conditions for the constraint to bind at the optimum
: Suppose a firm earns revenue R(Q) = aQ - bQ2 and incurs cost C(Q) = aQ + ßQ2 as functions of output Q = 0, where a, b, a, and ß are positive parameters.
|
|
Describe a brand that has earned your loyalty
: Describe a brand that has earned your loyalty. How, specifically, has the brand accomplished this?
|
|
Discuss the evolution of the program
: Discuss the role and relationship that exists among federal, state, and local governments in the administration of the program.
|
|
Are the demand functions homogeneous of degree zero
: Solve the consumer demand problem, max v(x) + v(y) subject to px + qy = m.
|
|
How do your triangles compare to each other
: How do your triangles compare to each other? Can you make your triangles look different from one another? Which postulate does this activity prove? Explain.
|
|
Write about the concept of servant leadership
: Choose another theory of leadership and compare and contrast the difference of that style of leadership with servant leadership.
|
|
Explain the solution geometrically of the admissible set
: The pair (x*, y*) that solves the problem in (a) also solves the minimization problem min (x2 + y2) subject to x - 3y = -10.
|
|
Provide the definition and meaning of each statement
: Create a mission, vision, and values statement for the retail clinic.Provide the definition and meaning of each statement.
|
|
Find the utility-maximizing demand functions
: Assuming that m > q2/4a2p, find the utility-maximizing demand functions x*(p, q, m, a) and y*(p, q, m, a), as well as the indirect utility function.
|