Reference no: EM131016892
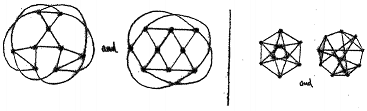
1. Are the following pairs of graphs isomorphic?
2. The double wheel Dn is constructed by taking the cycle Cn, then adding two new vertices u and v and edges from each of them to every vertex on the cycle. What is the degree sequence of Dn? How many vertices and edges does it have? Is Dn. connected?
3. Let G be a simple graph on 10 vertices and 38 edges. Prove that G contains K4 as an induced subgraph.
4. (a) Find all the non-isomorphic graphs whose degree sequence is (6, 3, 3, 3, 3, 3, 3).
(b) Find a labeled tree whose Prufer code is (2, 3, 4, 4, 3, 2, 1, 6, 5).
5. (a) Find the minimum spanning tree in each of the graphs below using Kruskal's algorithm.
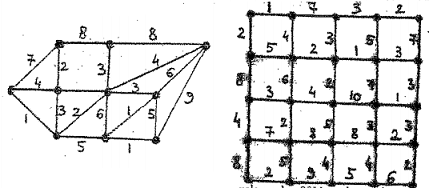
(b) Let G be a graph that is the union of a 2010-cycle and a 2011-cycle, with one common edge. Count the number of spanning trees of G.
6. (a) Find the number of 4-cycles in K2012, 2012.
(b) Compute the diameter and radius of K2012, 2012.
(c) Find the number of spanning trees of K2012, 2012.
7. The wheel graph Wn is defined as the join K1 V Cn. How many spanning trees does Wn have for n ≥ 3?
8. (a) Find α(G), α'(G), β(G) and β'(G) for the bipartite graph below.
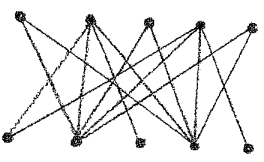
(b) Determine with proof whether the graph below has a perfect matching. If not, find the size of a maximum matching in that graph.
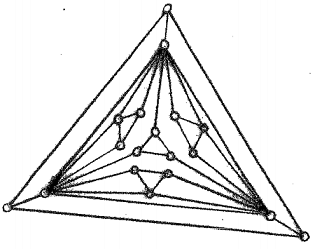
9. There are n children and n toys in a room. Each child wants to play with r specific toys, and for each toy, there are r children who want to play with that toy. Prove that we can organize r playing rounds so that in each of them, each child plays with a toy he/she wanted to, and no child plays with the same toy twice? (Contradicting real life a little bit, but not much, we assume that only one child can play with a toy at any one time.)
10. Alice and Bob play a game on a graph G alternately choosing distinct vertices. Alice starts by choosing any vertex. Each subsequent choice must be adjacent to the most recent choice of the other player. Thus, together they follow a path. The last player able to move wins. Who has a winning strategy that always works no matter how the other player plays?
|
How much of each ingredient will elizabeth need
: Elizabeth planned to make 6 pans of apple crisp for the day, using extra tart Granny Smith apples-just like her grandmother had. Based on her hasty decision, how much of each ingredient will she need?
|
|
Should they contact a policy maker
: A call to action that describes what you want readers to do. Should they contact a policy maker? Change their behavior? Join a group?
|
|
Find the length of the internal bisector of the right angle
: Find the length of the internal bisector of the right angle in a triangle with sides 3, 4, 5.
|
|
Classify the triangular shape of the sail
: The angles of a triangle sail measure 90°,30°,60°. it's sides measure approximately 2 feet, 3.5 feet , and4 feet. Classify the triangular shape of the sail in two different ways
|
|
Find the minimum spanning tree in each of the given graphs
: Find the minimum spanning tree in each of the graphs below using Kruskal's algorithm. Find all the non-isomorphic graphs whose degree sequence is (6, 3, 3, 3, 3, 3, 3).
|
|
Distribution and handle the rollover
: A trustee-to-trustee rollover is the preferred way to transfer one retirement account to another. All of these are potential problems when taxpayers take the distribution and handle the rollover themselves EXCEPT:
|
|
Difference between mean value added by the manufacturer
: Test to determine whether there is a significant difference between mean Value Added by the Manufacturer and the mean Cost of Materials in manufacturing. Use the Manufacturing database as the sample data and let alpha be .01. Use the Manufacturin..
|
|
Computing the net present value
: Lots of questions here, but it really is just one: what exactly is AFN?
|
|
What is the return on equity
: Oscar's Dog House has a profit margin of 5.6 percent, a return on assets of 12.5 percent, and an equity multiplier of 1.49. What is the return on equity?
|