Reference no: EM131107739

Honors Exam in Real Analysis 2010

1. In this problem, all matrices and vectors are given with respect to the standard basis.

a) Find the dimension of A²(R⁴), the space of alternating 2-tensors on R⁴.

b) Verify that the following map f: (R⁴)² → R is a member of A²(R⁴).

c) Compute

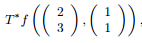
where f is as above and T: R² → R⁴ is the linear transformation given by the matrix

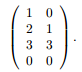
2. Let U ⊂ R^n-1 be an open set, and let α: U → Rⁿ be a smooth coordinate patch (in particular, α has Jacobian of rank n - 1 everywhere). Let g: Rⁿ → R be a smooth function such that g(y) = 0 and Dg(y) ≠ 0 for all y ∈ α(U).

a) Let f: Rⁿ → R be a smooth function, and supppose that the restriction of f to α(U) has a strict maximum: that is, there is some p ∈ α(U) such that

f(p) > f(q) for all q ∈ α(U) \ {p}.

Prove that Df(p) = λDg(p) for some real number λ.

b) Use part a) to find the maximum of the function f(x, y, z) = x + y + z on the set α(U), where U = {(x, y) : 0 < x < 1 and 0 < y < 1 }

and

α(x, y) = (x, y, 6x - 6x² + 3y - 3y²).

(Hint: Take g(z, x, y) = z - 6x + 6x² - 3y + 3y².)

3. In multivariable calculus, we learn about integration with polar coordinates. Here is a particular case: Suppose that U is an open bounded region in the x-y plane that is easily described in polar coordinates by a ≤ r ≤ b and c ≤ θ ≤ d - that is,

U = {(r cos(θ), r sin(θ)), r ∈ (a, b) and θ ∈ (c, d)},

where (a, b) ⊂ (0, ∞) and (c, d) ⊂ (0, 2π). Suppose that f: U → R is a smooth function. Then we have that

∫_Uf(x, y) = _c∫^d _a∫^b f(r cos(θ), r sin(θ))r dr dθ.

Give a rigorous justification for this formula.

-4. Let S² be the unit sphere in R³. Compute

∫_S^2 xz dx ∧ dy + 3y dx ∧ dz + y dy ∧ dz.

5. Let [a, b] be an interval in R, and let α : [a, b] → R² be a smooth coordinate patch (i.e. α is 1-to-1, smooth on (a, b), has nonzero Jacobian everywhere on (a, b), and has continuous inverse on its image).

Let us write γ = α((a, b)) for the image of α in R².

In advanced calculus we define the length of γ in two ways. One is the "surface measure" formula

∫_γ1 dS = _a∫^b det M(t),

where M(t) is the 2 × 2 matrix whose first column is Dα(t) (the Jacobian of α at t) and whose second column is the unit normal to γ at α(t), chosen so that det(M(t)) > 0.

The more common definition of the length of γ (as given, say, in Munkres' Analysis on Manifolds) is the "one-dimensional volume" formula

∫_γ1 dV = _a∫^b V (Dα(t)),

where

V(D(α(t)) = √(det [Dα(t)^trDα(t)].)

a) Show that these two definitions of the "length of γ" actually agree.

b) Rewrite the integral ∫_γ 1 dS as the integral of a 1-form on γ.