Reference no: EM132380532
Exercises 1:
(1994). The tidlist intersection based Eclat method is described in Zaki et al. (1997), and the dEclat approach that uses diffset appears in Zaki and Gouda (2003). Finally, the FPGrowth algorithm is described in Han, Pei, and Yin (2000). For an experimental comparison between several of the frequent itemset mining algorithms see Goethals and Zaki (2004). There is a very close connection between itemset mining and association rules, and formal concept analysis; see Ganter, Wille, and Franzke, 1997. For example, association rules can be considered to be partial implications with frequency constraints; see Luxenburger (1991).
Q1. Given the database in Table 8.2.
(a) Using minsup = 3/8, show how the Apriori algorithm enumerates all frequent patterns from this dataset.
(b) With minsup = 2/8, show how FPGrowth enumerates the frequent itemsets.
Q2. Consider the vertical database shown in Table 8.3. Assuming that minsup = 3, enumerate all the frequent itemsets using the Eclat method.
Table 8.2. Transaction database for Q1
| tid |
itemset |
| t1 |
ABCD |
| t2 |
ACDF |
| t3 |
ACDEG |
| t4 |
ABDF |
| ts |
BCG |
| t6 |
DFG |
| t7 |
ABG |
| t8 |
CDFG |
Table 8.3. Dataset for Q2
| A |
B |
C |
D |
E |
| 1 |
2 |
1 |
1 |
2 |
| 3 |
3 |
2 |
6 |
3 |
| 5 |
4 |
3 |
|
4 |
| 6 |
5 |
5 |
|
5 |
|
6 |
6 |
|
|
Q3. Given two k-itemsets Xa, = {x1,...,xk-1,xa} and Xb, = {x1,...,xk-1, xb} that share the common (k - 1)-itemset X = {x1,.x2,...,xk-1} as a prefix, prove that
sup(Xab) = sup(Xa) - |d(Xab)| where Xab = Xa U Xb and d(Xab)) is the diffset of Xab.
Q4. Given the database in Table 8.4. Show all rules that one can generate from the set ABE.
Table 8.4. Dataset for Q4
| tid |
itemset |
| t1 |
ACD |
| t2 |
BCE |
| t3 |
ABCE |
| t4 |
BDE |
| ts |
ABCE |
| t6 |
ABCD |
Q5. Consider the partition algorithm for itemset mining. It divides the database into k partitions, not necessarily equal, such that D = Ui=1kDi, where Di is partition i, and for any i ≠ j, we have Di ∩ Dj = Ø. Also let ni = |Di| denote the number of transactions in partition Di. The algorithm first mines only locally frequent itemsets, that is, itemsets whose relative support is above the minsup threshold specified as a fraction. In the second step, it takes the union of all locally frequent itemsets, and computes their support in the entire database D to determine which of them are globally frequent. Prove that if a pattern is globally frequent in the database, then it must be locally frequent in at least one partition.
Exercises 2: Summarizing Itemsets
The concept of closed itemsets is based on the elegant lattice theoretic framework of formal concept analysis in Ganter, Wille, and Franzke (1997).The Charm algorithm for mining frequent closed itemsets appears in Zaki and Hsiao (2005), and the GenMax method for mining maximal frequent itemsets is described in Gouda and Zaki (2005). For an Apriori style algorithm for maximal patterns, called MaxMiner, that uses very effective support lower bound based itemset pruning see Bayardo Jr (1998). The notion of minimal generators was proposed in Bastide et al. (2000); they refer to them as key patterns. Nonderivable itemset mining task was introduced in Calders and Goethals (2007).
Q1. True or False:
(a) Maximal frequent itemsets are sufficient to determine all frequent itemsets with their supports.
(b) An itemset and its closure share the same set of transactions.
(c) The set of all maximal frequent sets is a subset of the set of all closed frequent itemsets.
(d) The set of all maximal frequent sets is the set of longest possible frequent itemsets.
Q2. Given the database in Table 9.1
(a) Show the application of the closure operator on AE, that is, compute c(A£). Is AE closed?
(b) Find all frequent, closed, and maximal itemsets using minsup = 2/6.
Q3. Given the database in Table 9.2, find all minimal generators using minsup = 1. Exercises 257
Table 9.1. Dataset for Q2
| tid |
itemset |
| t1 |
ACD |
| t2 |
BCE |
| t3 |
ABCE |
| t4 |
BDE |
| ts |
ABCE |
| t6 |
ABCD |
Table 9.2. Dataset for Q3
| tid |
itemset |
| 1 |
ACD |
| 2 |
BCD |
| 3 |
AC |
| 4 |
ABD |
| 5 |
ABCD |
| 6 |
BCD |
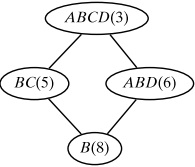
Figure 9.7. Closed itemset lattice for Q4.
Q4. Consider the frequent closed itemset lattice shown in Figure 9.7. Assume that the item space is I = {A, B, C, D, E}. Answer the following questions:
(a) What is the frequency of CD?
(b) Find all frequent itemsets and their frequency, for itemsets in the subset interval [B, ABD].
(c) Is ADE frequent? If yes, show its support. If not, why?
Q5. Let C be the set of all closed frequent itemsets and M the set of all maximal frequent itemsets for some database. Prove that M ⊆ C.
Q6. Prove that the closure operator c = i o t satisfies the following properties (X and Y are some itemsets):
(a) Extensive: X ⊆ c(X)
(b) Monotonic: If X ⊆ c(Y) then x(X) ⊆ c(Y)
(c) Idempotent: c(X) = c(e(X))
Exercises 3:
time algorithm. The total time over the entire database of N sequences is thus O(Nn), ifn is the longest sequence length.
The level-wise GSP method for mining sequential patterns was proposed in Srikant and Agrawal (1996). Spade is described in Zaki (2001), and the PrefixSpan algorithm in Pei et al. (2004). Ukkonen's linear time suffix tree construction method appears in Ukkonen (1995). For an excellent introduction to suffix trees and their numerous applications see Gusfield (1997); the suffix tree description in this chapter has been heavily influenced by it.
Q1. Consider the database shown in Table 10.2. Answer the following questions:
(a) Let minsup = 4. Find all frequent sequences.
(b) Given that the alphabet is ∑ = {A,C,G,T}. How many possible sequences of length k can there be?
Table 10 2. Sequence database for Q1
|
Id
|
Sequence
|
|
s1
|
AATACAAGAAC
|
|
s2
|
GTATGGTGAT
|
|
s3
|
AACATGGCCAA
|
|
S4
|
AAGCGTGGTCAA
|
Q2. Given the DNA sequence database in Table 10.3, answer the following questions using minsup = 4
(a) Find the maximal frequent sequences.
(b) Find all the closed frequent sequences.
(c) Find the maximal frequent substrings.
Attachment:- Exercises.rar