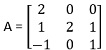Reference no: EM132688106

Question 1: Find the eigenvalues and bases for the eigenspace of the matrix

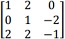
Question 2: Suppose that T: R³ → R³ is a linear transformation so that

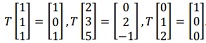
 (a) Find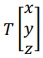

(b) Find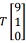

Question 3: Let T: P2 → P2 by

T(ax² + bx + c) = (4b + a)x² + (c - a)x + (3c - b - a);

α the standard basis for P2; β the basis consisting of

2x² + 3x, x²+5, x+7; v=2x²+7x - 3

(a) Find [T]_a^a where a is the standard basis for P₂.

(b) Find the change of basis matrix from a to β.

(c) Find the change of basis matrix from β to a.

(d) Find [T]_β^β

(e) Find [v]_β 

(f) Find [T(v)]_β.

(g) Find T(v).

Question 4: Determine whether the given matrix A (3×3) is diagonalizable and, if it is, give a diagonal matrix similar to A as well as a matrix P and its inverse so that P^-1 AP is this diagonal matrix.