Reference no: EM132352687

Assessment -

Answer all questions. Please submit working and answers via loop.

Q1. Select the correct inverse Laplace Transform of 12/(s²+4s+20)

3u(t)e^-2tsin4t

3u(t)e^2tsin4t

12u(t)e^-2tsin4t

12u(t)e^2tsin20t

None of the these

Q2. Which of the following is the approximate period (in seconds) of the function g(t) = cos(8t) + 2 cos(12t) - 3 sin(20t)?

8s

3.142s

0.785s

1.571s

None of the these

Q3. Select the correct result for the following integration _-∞∫^∞2^tδ(t - 3)dt.

8

6

5

2

None of the these

Q4. Given that the Fourier transform of u(t)e^-t is 1/(1+jω), use the duality principle to deduce the transform of 1/(1+jt).

2π(u(-ω)e^ω)

2π(u(ω)e^-ω)

1/2π(u(-ω)e^ω)

1/2π(u(ω)e^-ω)

None of the these

Q5. Select the correct convolution result of f ∗ g when f(t) = u(t)e^-t and g(t) = u(t)e^-2t.

u(t)e^-3t

u(t){e^t - e^2t}

u(t){e^-t - e^-2t}

u(t)e^3t

None of the these

Q6. Select the correct inverse Fourier transform of 20((sin 10ω)/10ω).

u(t + 10) - u(t - 10)

u(t + 20) - u(t - 20)

20{u(t + 10) - u(t -10)}

20{u(t +20) - u(t - 20)}

None of the these

Q7. Select the correct function whose Fourier transform is 1/(1+j(ω-7)).

u(t)e^(1+7j)t

u(t)e^-(j+7)t

u(t)e^-(j-7)t

u(t)e^-(1-7j)t

None of the these

Q8. Let

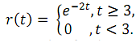
k(t) is r(t) advanced (shifted left) by 3 seconds. Select the correct expression for the Fourier Transform K(ω) of k(t). Hint: Sketch the function.

e^-6/(jω + 2)

e^-3/(jω + 2)

e³/(jω + 2)

e⁶/(jω + 2)

None of the these

Q9. y(t) is as shown in the figure. Which of the following is the Fourier transform of y(t)?

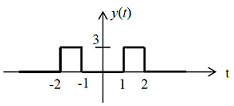
12/ω{sin(2ω) - sin(ω)}

6/ω{sin(2ω) - sin(ω)}

3/ω{sin(2ω) - sin(ω)}

4sinc(2ω)

None of the these