Reference no: EM132389562

For Problems 1, 2, and 3, H, P and L are subspaces of R⁴ defined by

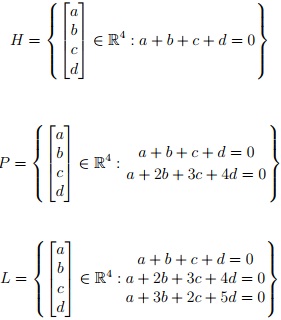
Question 1. Find three vectors u₁, u₂, u₃ ∈ R⁴ satisfying the following properties:

{u₁, u₂, u₃} is an orthonormal set, {u₁} is a basis for L, {u₁, u₂} is a basis for P , and u₁, u₂, u₃ is a basis for H. These bases will be useful for solving Problems 2 and 3.

Question 2. Let T : H → H be the linear transformation that rotates all points in H by 30° counterclockwise about the line L. Find a 4 × 4 matrix A such that

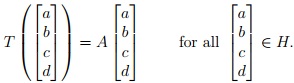
Note that you will have to use the more general definition of angle in R⁴ that is expressed in terms of the dot product and the arccosine function.

Question 3. Let T : P → P be the linear transformation that reflects all points in P about the line L. Find a 4 × 4 matrix A such that

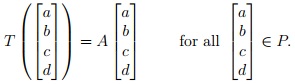
Question 4. Let T : R⁵ → R⁶ be the linear transformation defined by

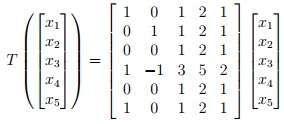
(a) Find a basis for the kernel of T.
(b) Find a basis for the image of T.
(c) Is T injective? If so, prove this. If not, give an example of two distinct input vectors giving rise to the same output vector.
(d) Is T surjective? If so, prove this. If not, give an example of a vector in R⁶ that is not the image of any vector in R⁵.

Question 5. Let

V = {p(x) : deg p(x) ≤ 4 and p(2) = 0 and p(3) = 0}.

Define T : V → V by
T (x) = (x - 2)(x - 3)p'''(x).

(a) Find a basis for V .
(b) Find a matrix representation for T with respect to the basis in (a).
(c) Prove that T is neither injective nor surjective.