Reference no: EM132383358

ENGR 122 Engineering Mathematics with Calculus Assignment - Victoria University of Wellington, New Zealand

Lab - Spin Doctor Respun

Aim - This lab exercise is a follow-up to the Spin Doctor lab in ENGR 121. We will review a bit and then work through some harder problems. Our goals are:

1) Understanding rotation, translation, reflection, and the matrices that implement these operations.

2) Working with matrices

3) Developing familiarity and skill with trig identities.

Review and getting Python ready - The appendix at the end of the lab script has some notes about matrices in Python. Read through it for review. Include your Python work in your answers for the remainder of the lab. It is probably easiest to work in a text editor and paste into Python so you can reuse chunks of code.

You will need to import math and matrix functions:

Use from numpy import math, from numpy import matrix, from numpy.linalg import inv.

The Rotation Matrix - This is your basic rotation matrix. It rotates a point counterclockwise in the XY plane by angle:

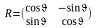
Let's take this matrix out for a spin. We will start with the point (0,-1) and rotate it 270 degrees, and find out where it ends up.

Hints: Try this. Use a text editor. You can copy and paste this and then modify it for other parts of the lab. Remember to use ctrl-shift-v to paste in Python. Here is what you would do to create a matrix that rotates by pi. You can adapt that to your needs.

R = (math.cos(math.pi), -math.sin(math.pi), math.sin(math.pi), math.cos(math.pi))

R=matrix(R).reshape(2,2)

P=(0,-1)

P=matrix(P).reshape(2,1)

print(R*P)

Hint: Don't forget to use radians rather than degrees throughout the lab.

CORE 1 - Verify two basic properties of rotations for at least one example in each case.

(1) A rotation by θ+2nπ is the same as rotation by θ.

(2) Rotation by θ and then by -θ gets you back where you started.

CORE 2 - Now let's work on a non-square rectangle. Your rectangle is (1,1) (4,1) (1,3) (4,3). Rotate it so that it is in the third quadrant. Hint: rotate each point.

COMPLETION 1 - Now we will work with our rotation matrix algebraically. You can work on a sheet of paper and upload a photo of your work. Use the definition of the rotation matrix, matrix multiplication, and trig identities show that a rotation by an angle θ₁ and then θ₂ is the same as a rotation by θ₁+θ₂.

COMPLETION 2 - Find the inverse of R(ϑ) and compare the result to R(-ϑ). How is this related to our results in Completion 1? Note this was a superchallenge in the 121 lab.

The Reflection Matrix - To reflect a point across a line through the origin and another point (x,y) we use

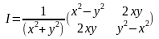
COMPLETION 3 - Show that for reflecting across the x axis this reduces to

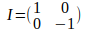
COMPLETION 4 - Reflect the point (1,2) across a line at pi/6 radians above the x axis. Make a quick sketch of the point before and after reflection. Is the operation behaving as expected?

Combining Operations - The stretch matrix below with stretch an object along the x axis by factor s.

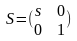
CHALLENGE 1 - Stretch your rectangle along the y direction by a factor of 2, rotate it clockwise by 45 degrees, and shift it to the right by 3. Include your python code and make rough sketches of the rectangle before and after the transformations. Hint: translation can be accomplished by adding a vector or by using a 3x3 matrix with homogeneous coordinates (CGRA students). Did you get what you expected?

CHALLENGE 2 - When you rotated your rectangle (CORE 2) it rotated around the origin. Now make it rotate around its own centre.

Attachment:- Engineering Mathematics with Calculus Assignment File.rar