Reference no: EM131081571
Math 104: Homework 8- Curve sketching
At this point in the class, being able to sketch functions and determine their properties is an important skill, which will greatly help in understanding concepts such as continuity, differentiability, and uniform convergence. Therefore, this week's homework is mainly devoted to this topic.
In the following questions, no detailed proofs are required, although you will need to provide some discussion in words about what is going on. To begin, I would like you to try and draw the graphs by hand. There are many ways to do this, such as looking at the behavior as x → ±∞, calculating a few specific points and drawing a line through them, using calculus, or searching for zeroes of the function.
After this, you can confirm your results using a plotting program. There are many free ones available, such as Gnuplot (www.gnuplot.info), which runs on Windows, Mac, and Linux.
1. Consider the function
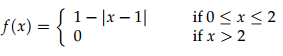
defined on the interval [0, ∞)†. Draw f(x).
(a) Draw f(x/2), f(x/3), and f(x/4), and explain how the shapes of these curves relate to f(x).
(b) Draw 2 f(x), f(x + 1/2), f(x) - 1/2 and explain how the shapes of these curves relate to f(x).
(c) Draw | f(x) - 1/2|. Is this function continuous? Is it differentiable everywhere?
(d) Draw f(x2) and f(x)2.
2. Consider the sequence of functions
fn(x) = nx2/1 + nx2
defined on the interval [0, ∞).
(a) Begin by considering f1(x). How does it behave as x → ∞? How does it look close to x = 0? Use these facts to draw f1(x).
(b) Show that fn(x) = f1(√nx). By considering question 1(a), use this fact to draw several of the fn(x).
(c) It can be shown that fn converges pointwise to a function f defined on [0, ∞) as
Draw f(x) and draw a strip of width ε = 1/4 around f(x). If fn → f uniformly, then there exists an N such that n > N implies that fn lies wholly within this strip. Use the graph to explain in words why no such N exists, so that fn does not converge uniformly to f.
3. Consider the sequence of functions defined on R as
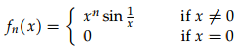
(a) Draw the sequence of functions f0(x), f1(x) and f2(x). Which of the functions are continuous at x = 0? Which of them are differentiable at x = 0?
(b) Consider the functions fn on the interval [-1/2, 1/2], and define f(x) = 0. By considering a strip of width e around f(x), explain why fn will converge uniformly to f on this interval.
4. Plot the functions
- f1(x) = x2(x - 1)(x - 2)
- f2(x) = |f1(x)|
- f3(x) = x/1+x2
- f4(x) = |x| + |x - 2|
- f5(x) = |x| - 2|x - 1| + |x - 2|
For each function, write down any values of x where it is not differentiable.
5. Consider the function g0(x) = |x| on R. For n ∈ N, define gn(x) = |gn-1(x) -21-n|.
(a) Draw g0(x), g1(x), g2(x), and g3(x).
(b) Optional for the enthusiasts. Prove that the functions gn converge uniformly to a limit g on R.