Reference no: EM132312145

Assignment -

Question 1 -

a. Draw sketches of the following regions in the complex plane:

i. |z-2i| = 4

ii. Im(z²) = 1, - π/2 < arg(z) < π/2

b. Use the definitions of cosh(z) and sinh(z) to show

cosh(π/2 i - z) = sinh(z)/i

c. Find all solutions for z of cos z = 2i

d. Find all values for the following expressions. Also identify the principal value. Put all values in the form a + ib

i. (-i)^1/4

ii. (cosi)ⁱ

iii. log(1-i)

Question 2 -

a. Determine, if possible, the following limits

i. lim_z→0(z-z^-)²/|z|²

ii. lim_z→0(e^z-1)/sinz [Use Taylor series, or any other available method].

b. Let u(x, y) = xy + cosh x sin y

i. Show u(x, y) is harmonic.

ii. Find a harmonic conjugate, v(x, y) of u(x, y).

iii. Find a function, f(z) such that Re(f(z)) = u(x, y).

iv. Calculate the derivative, f'(z).

Question 3 -

a. Let C be the curve given in the following diagram:

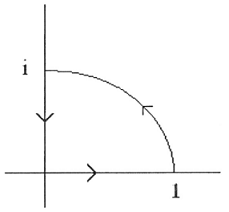
[C is a straight from 0 to 1, then goes from 1 to i along the circle centred at the origin with radius 1. It then follows a straight line back to the origin.]

Calculate

i.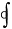_C z²dx

ii. 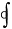_C z^{-^2} dz

b. Find 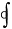_|z|=2 (2z³+iz)/(z+i)³ dz [Note: the counter is |z| = 2]

c. Find 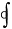_|z|=1/2 sinhz/(z⁴-1) dz [Note: the counter is |z| = 1/2]

Question 4 -

a. Let f(z) = 1/(z²-1)

i. Find the Laurent series for which f(z) converges for 0 < |z+1| < 2.

ii. Find the Taylor series of f(z) about z = i and state the region where the series converges.

b. Find the Laurent series for z³ cos(1/z) in powers of z. What is the nature of the singularity at z = 0?

Question 5 -

a. Evaluate the following integrals [note: the contour is |z| = 2]:

i. 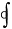_|z|=2 z³ cos(1/z)dz

ii. 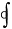_|z|=2z/(z2+z+1)dz

b. Show ₀∫^π 8dθ/(5+2cosθ) = 1/i 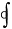_|z|=1 4dz/(z2+5z+1) and hence evaluate the integral.

c. Evaluate, using residue calculus:

_-∞∫^∞ dx/((x²+4)(x²+1))