Reference no: EM132264344

Question 1. Define a sequence of numbers S_n (for integers n ≥ 0) recursively as follows:

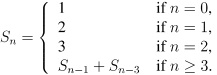
(a) Prove by induction that Σⁿ_i=3S_i-3 = S_{n - 3} for all integers n ≥ 3. No credit will be given for a different method of proof.

(b) Prove by induction that S_n+3 ≥ Φⁿ for all integers n > 0, where Φ ∈ (1, 2) is a root of the equation x³ - x² - 1 = 0. No credit will be given for a different method of proof.

(Remark: Such Φ exists and here is an argument to show why: If we let f (x) = x³ - x² - 1, we have f (1) < 0 and f (2) > 0, and thus the equation 1 (x) = 0 has a solution (root) in the range (1, 2) and we call this root Φ - this is just a background information and you do not need to worry about this part.)

Question 2. What is wrong with the following purported proof that all horses have the same color?

Proof by induction on the number of horses:
Basis Step. There is only one horse. Then clearly all horses have the same color.
Induction Hypothesis. In any group of up to n horses, all horses have the same color.
Induction Step. Consider a group of n + 1 horses. Discard one horse; by the induction hypoth-esis, all the remaining horses have the same color. Now put that horse back and discard another; again all the remaining horses have the same color. So all the horses have the same color as the ones that were not discarded either time, and so they all have the same color.

Question 3. Consider the following sequence of items

10, 36, 25, 54, 37, 12, 75, 68, 42, 86, 72, 90.

Insert these items in the order above, into an initially empty implicit binary max-heap. Show the heap after every 3 INSERTO operations. (Just hand-simulate the behavior of the standard implicit binary max-heap, and draw the resulting heap after every 3 INSERT() operations.

Draw them in the form of a tree rather than an array.)

Question 4.

Consider the implicit binary heap with the array representation where the root is indexed by 1. Prove that when there are n elements in the heap, the leaves are the nodes indexed by [n/2] + 1, [n/2] + 2, .... , n.

Question 5.

Consider an implicit binary max-heap A storing n items in an array, where A[1] is the root and stores the maximum item. Assume that all keys stored in A are distinct.

(a) Suppose we want to support an additional operation SEARCH(A, k): for a given key k, return the index i such that A[i] = k, or report "none" if no such key k is stored in A. Give an example to show that in the best case, SEARCH() can be performed in 0(1) time. Also, give an example to show that in the worst case, SEARCH() needs C2(n) time. Finally, give a simple algorithm to carry out SEARCH() in 0(n) worst-case time (which is thus optimal).

(b) Suppose we want to support another operation DELETE(A, i): given an integer i e [1, n], delete the item A[i] (and still maintain A to be an implicit binary max-heap after the deletion). Give a direct algorithm (i.e., not using any existing operations) to carry out the task, and analyze its run-ning time. Your algorithm should run in 0 (log n) worst-case time. (8 points)

Question 6.

Implicit binary heap implemented by an array is simple and efficient, except that at some point when the array is full and an INSERT() operation comes in, we need to re-allocate a larger array (allocating a new, larger memory space, copying the data items over, and releasing the old memory space), which is expensive. A natural alternative is to implement a binary heap as a binary tree where each node has pointers to its parent, left child and right child. Again, it is a complete binary tree except for the lowest level, which is filled from the left up to some point. Now the key task here is to be able to find the last node efficiently.

(a) We can represent a path from the root to a node of a binary tree by means of a binary string (e.g., "01101"), where 0 means "go to the left child" and 1 means "go to the right child." Based on this representation, design and analyze an algorithm to find the last node of an n-node binary heap in 0 (log n) time.

(Hint: Look at small examples to derive your algorithm and also to check whether your algorithm is correct or not.)

(b) Discuss how to incorporate the algorithm in part (a) into the operations EXTRACT_MIN(Q) (extracting the minimum element from Q) and INSERT(Q, x) (inserting an element x into Q) for a binary min-heap Q.

Question 7.
Given an implicit binary max-heap A in an array (where the root A[1] stores the maximum item), a real number x and a positive integer k, design and analyze an algorithm to decide whether the k-th largest item in A is ≥ x. Your algorithm should run in O(k) worst-case time and use at most O(k) extra space, independent of the size of A.

Note: Your algorithm does not need to report the k-th largest item in A; only its relationship with x needs to be decided, to be able to answer "yes" or "no".