Reference no: EM131514243

1. Suppose a random variable is equally likely to fall anywhere in the interval [a, b]. Then the PDF is of the form

Find and sketch the corresponding CDF.

2. Find and plot the CDFs corresponding to each of the following PDFs:

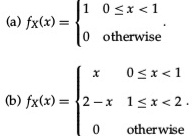
3. A random variable has the following exponential PDF:

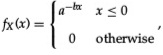
where a and b are constants.

(a) Determine the required relationship between a and b.
(b) Determine the corresponding CDF.

4. A certain random variable has a probability density function of the form fx(x) = ce^-2xu(x). Find the following:
(a) the constant c,
(b) Pr(X > 2),
(c) Pr(X < 3),
(d) Pr(X < 3|X > 2).

5. Repeat Problem 4 using the PDF f_x(x) = c/(x² +4)

6. Repeat Problem 4 using the PDF f_x(x) = c/(√25 - x²)' -5 < x < 5.

7. The voltage of communication signal S is measured. However, the measurement procedure is corrupted by noise resulting in a random measurement with the PDF shown in the accompanying diagram. Find the probability that for any particular measurement, the error will exceed ±0.75 percent of the correct value if this correct value is 10 volts.

8. Prove the integral identity, I = _-∞∫^∞ exp(- x²/2)dx = √(2Π) Hint: It may be easier to show that  I² = 2Π.

9. Using the normalization integral for a Gaussian random variable, find an analytical expression for the following integral:

I = _-∞∫^∞ exp-(ax² + bx + c))dx,

where a > 0, b, and c are constants.

10. A Gaussian random variable has a probability density function of the form

f_x(x) = c exp(-(2x² + 3x + 1)).

(a) Find the value of the constant c.

(b) Find the values of the parameters m and o for this Gaussian random variable.

11. A Gaussian random variable has a PDF of the form

f_x(x) = 1/√(50Π) exp (-(x - 10)²/50)

Write each of the probabilities in terns of O-functions

(a) Pr(X > 17)

(b) Pr(X > 4)

(c) Pr(X < 15)

(d) Pr(X < -2)

(e) Pr(|X -10| > 7)

(f) Pr(|X - 10| <3)

(g) Pr(|X- 7| > 3)

(h) Pr(|X - 4| <7)

12. Prove the following properties of the Gamma function.
(a) Γ(n) = (n - 1)!, for n = 1, 2, 3, ...
(b) Γ((x +1) = xΓ(x)
(c) Γ(1/2) = √Π

13. Prove the following properties of conditional CDFs.
(a) F_x|A(-∞)= 0, F_x|A(∞) = 1
(b) 0 ≤ F_x|A(x) ≤ 1
(c) For x₁ < x₂, F_x|A(x₁) ≤ F_x|A(x₂)
(d) For x₁ < x₂, Pr(x₁ < X ≤ x₂|A) = F_x|A(x₂) - F_x|A(x₁)

14. Let X be a Gaussian random variable such that X~N(0, σ²). Find and plot the following conditional PDFs.
(a) f_x|x>0 (x)
(b) f_x||x|<3(x)
(c) f_x||x|>3(x)

15. Mr. Hood is a good archer. He can regularly hit a target having a 3-ft. diameter and often hits the bull's-eye, which is 0.5 ft. in diameter, from 50 ft. away. Suppose the miss is measured as the radial distance from the center of the target and, further, that the radial miss distance is a Rayleigh random variable with the constant in the Rayleigh PDF being σ² = 4(sq. ft.).

(a) Determine the probability of Mr. Hood's hitting the target.
(b) Determine the probability of Mr. Hood's hitting the bull's-eye.
(c) Determine the probability of Mr. Hood's hitting the bull's-eye given that he hits the target.

16. A digital communication system sends two messages, M = 0 or M = 1, with equal probability. A receiver observes a voltage which can be modeled as a Gaussian random variable, X, whose PDFs conditioned on the
(a) Find and plot Pr(M = 0|X = x) as a function of x for σ² = 1. Repeat for σ² = 5.
(b) Repeat part (a) assuming that the a priori probabilities are Pr(M = 0) = 1/4 and Pr(M = 1) = 3/4.

17. In Problem 16, suppose our receiver must observe the random variable X and then make a decision as to what message was sent. Furthermore, suppose the receiver makes a three-level decision as follows:
(1) Decide 0 was sent if Pr(M = 0|X = x) ≥ 0.9.
(2) Decide 1 was sent if Pr(M = 1|X = x) ≥ 0.9.
(3) Erase the symbol (decide not to decide) if both Pr(M = 0|X = x) < 0.9 and Pr(M = 1|X = x) < 0.9.

Assuming the two messages are equally probable, Pr(M = 0) = Pr(M = 1) = 1/2, and that σ² = 1, find
(a) the range of x over which each of the three decisions should be made,
(b) the probability that the receiver erases a symbol,
(c) the probability that the receiver makes an error (i.e., decides a 0 was sent when a 1 was actually sent, or vice versa).

18. Recalling Example 15, suppose that a serial connection system has 10 components and the failure rate function is the same constant for all components and is 1 per 100 days.
(a) Determine the probability that the lifetime of the system exceeds 10 days.
(b) What is the probability that the lifetime of one component exceeds 10 days?
(c) What is the reliability function of each component and of the system as a whole?