Reference no: EM132515470

Problem 1 Identify the correct description for the formula

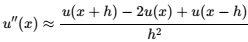
from the following options:

FFD1: forward finite difference with stepsize h for the first derivative of u at x
BFD1: backward finite difference with stepsize h for the first derivative of u at x
CFD1: central finite difference with stepsize h for the first derivative of u at x
CFD2: central finite difference with stepsize h for the second derivative of u at x None of the Above

Problem 2.
Specify c_-1, c₀, c₁ and p such that the formula
g′(s) ≈ h^-p(c_-1g(s - h) + c₀g(s) + c₁g(s + h))
denotes the central finite difference for the first derivative of g with step size h. Use decimal notation to enter any fractions.

Problem 3.

Given the formula

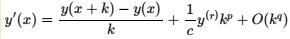
use the Taylor series

to determine the integer values of c, p, q and r. (Note that integer values can be positive, negative or zero. Do not forget to include the minus sign for any negative values.)

Problem 4.

Given the function

v(s) = cos(4 - sin(3s))

and the mesh s_i = s₀ + ik, where s₀ = -Π/3 ,

determine the backward finite difference for the first derivative of v with step size k = 15 at mesh point i = 4. At the same point, also calculate the exact first derivative v′(si).

Calculate the absolute value of the error of the finite difference approximation at the point s_i.

Work to at least 6 decimal places throughout and enter your answers to 2 decimal places.

(a) Enter the finite difference approximation

(b) Enter the exact derivative

(c) Enter the absolute error

(d) If we were to divide the step size by 2, the error will be approximately multiplied by a factor of

Problem 5.

Given the tridiagonal matrix

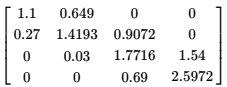
work out the values li, i = 1, ... , 4 and ui, i = 1, ... , 3 in the LU factorisation A = L U with

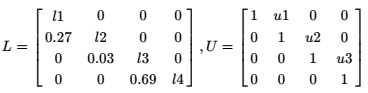
Use the LU factorisation to solve the system Ax = b with

Use at least 6 decimal places for your calculations and specify your final results to 2 decimal places.