Reference no: EM132323733

Assignment : Basic Skills Review

Question 1

Rewrite the following relationships using function notation.

a) An airplane needs to travel 400 km. Determine a function for the speed of the airplane, with respect to time.

b) An ice cream cone is left sitting in the hot sun. Sarah notices that the ice cream melts and loses half of its volume every 5 minutes. If the starting volume was 125 mL, determine a function for the volume, with respect to the amount of time left out in the sun.

c) Scott wants to calculate the distance from his house to each of his friends' houses. If he drives at 50 km/h, find a function for the distance, with respect to the number of hours it takes to travel.

Question 2

Find the inverses of each of the functions below algebraically.

p (r)=2r²+2r-1

3y + 5x=18

h(t) = -4.9(t + 3)² + 45.8

Question 3

With the aid of graphs, explain whether or not the inverses in question 2 are functions.

Question 4

For each of the functions below, state the domain and range, the restrictions, the intervals of increasing and decreasing, the roots, y-intercepts, and vertices.

a) ƒ(x) = 3x² -8

b) ƒ(x) = +√(x-2)

c) ƒ(x) =(∞+1)/(∞-1)

Question 5

The point (1,-2) is on the graph of f (x). Describe the following transformations on f (x), and determine the resulting point.

a) g (x)= 2 ƒ(x) + 3

b) g(x) = ƒ(x + 1) - 3

c) g (x)= - ƒ(2x)

d) g(x) = -ƒ(-x -1) + 3

Question 6

Create a multimedia presentation to explain your reasoning behind one of your solutions to Question 3.

Unit Assignment: Polynominal Functions

Question 1

Without graphing, answer the following questions for each of the functions below:

i. What are the end behaviours of this type of function (what quadrant does it begin and end in?)

ii. What is the maximum and minimum number of x-intercepts for this type of function?

iii. What is the maximum and minimum number of turns for this type of function?

iv. State if there are any restrictions on the domain and range on this type of function.

It may be easiest to format your answer by setting up a chart with the headings "End Behaviours, Maximum number of x-intercepts, Minimum number of x-intercepts, Maximum number of turns, Minimum number of turns, and Restrictions'', then filling in your answers for the functions listed.

a) ƒ(x) = 3x³ kx² 6x 4- 8

b) ƒ(x) = -x⁴ - 6x³ + k,x - 24

c) ƒ(x)= x⁵ - kx⁴ 21x³ ± 72

Question 2

Using the graphs provided, determine the equation for the polynomial function being represented. Show all of your work.

(a)

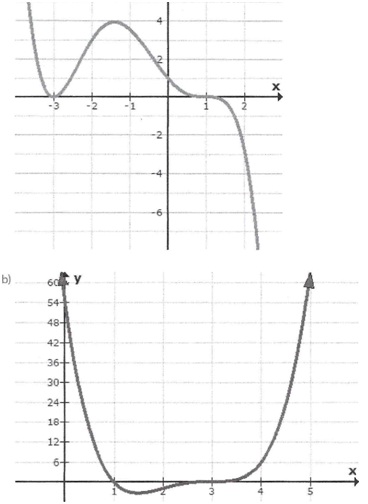
Question 3

Using the table of values given, determine the equation of the function that would model this data.

x	ƒ(x)
1	-36
2	0
3	-32
4	-54
5	-60
6	-44

Question 4

Determine if the following polynomial functions have even or odd symmetry, or neither. Justify your reasoning.

a)  ƒ(x) = x² - x - 6

b)  ƒ(x) = x² + 4^x4

c)  ƒ(x) = x + x³

d) ƒ(x) = 2x³ + 4x

Question 5 

Factor each of these polynomial functions completely. Show all of your work.

a) ƒ(x)= x³ - 13x + 12

b) ƒ(x)= -5x³ + 17x² - 16x + 4

c) ƒ(x)= 5x⁴ - 22x³ + 33x² - 20x + 4

Question 6

Using what you have learned in this unit, solve the following problem:

The profit of a company can be modelled by the polynomial function P (t) = -t³ + 12t² - 21t + 10

, where P is the profit, in thousands of dollars, and t is the time, in years. When will the company make their maximum profit of $108 000?

Question 7

The thickness of the ice on a lake for one week is modeled by the function:

T (d) = -0.1d³ + 1. 2d² - 4.4d + 14.8

where T is the thickness in cm and d is the number of days after December 31st.

a) Graph this function using graphing technology. Ensure your axes are properly set up, and state the domain and range that are appropriate for the situation. When do you think the warmest day occurred during the week? Justify your answer, then determine the average rate of change on a short interval near the point you chose.

b) Determine the instantaneous rate of change at this point.

c) Are the rates you calculated in a) and b) the same or different? Why do you think this is?

Unit Assignment: Trigonometry

Question 1

a) Find all solutions for 2 cos (x) =√3

b)If sin (x) =1/3 and sec (y) = 5/4 where 0 ≤ x ≤ Π /2 and 0 ≤ y ≤ Π /2 evaluate the expression sin (2y) .

Question 2

Solve for all values of x in the given intervals:

a) 8 tan(x) + 11 = 19 for 0 ≤ x ≤ 2Π

b) sec² (x) = 2 tan² (x) for ∈ R

c) sec² (x) + sec² (x) - 1 = 3 for x ∈ R

Question 3

Prove the following identities:

(if it is a one step problem please state the formula used)

a) sin (Π /2 + x) = cos (x)

b) sin (x) cot (x) = cos (x)

c) cot² (x) + sec² (x) = tan² (x) + csc² (x)

d) sin² (x) - sin²(y) = sin (x+y) sin (x-y)

Question 4

Describe how to use both an equivalent trigonometric identity and a diagram to demonstrate that two trigonometric ratios are equivalent.

a) Use one of the following equivalent trigonometric expressions:

sin (Θ +3Π/2) = -cosΘ

cos (Θ +3Π/2) =  sinΘ

tan (Θ +3Π/2) =  -cotΘ

sin (3Π/2-Θ) = - cosΘ

cos (3Π/2-Θ) = - sinΘ

tan (3Π/2-Θ) = cotΘ

b)  Using a diagram demonstrate how the related angle formulas are true. Create an example to illustrate your findings in part a) (choose a value for and solve both sides to prove that they are equal.)

Unit Assignment: rational Functions and Inequalities

Question 1

a) What is a rational function?

b) How is it different from a polynomial?

c) Provide a graph of each to demonstrate the difference.

Question 2

For the following functions, find:

i) x-intercept

ii) y-intercept

iii) Holes

iv) Vertical Asymptotes

v) Horizontal/Oblique Asymptotes

vi) The end behaviours

vii) Defining Intervals

viii) Sketch by hand

a) ƒ(x) = 5/ (x-2)

b) ƒ(x) = x²/(2x-5)

c) ƒ(x) = (2x²-5x+4)/(x²-4)

Question 3 

Find the values that satisify the given equations:

a) (2x²+11x-6) /(x³ -2x+6)=0

b) x (2x + 19) < 10

c) 1/2<  (x²-7x+10)-(1/2x)

Question 4 

In South America, a rare species of spiders is discovered and is transplanted into a safe area. Once they are transported the population of the spider after t months is

P(t) =  44 (1 + 0.7t) / (3 +0.03t)

a) What was the population at t=0?

b) What will the population be after 15 years?

c) When will there be 652 spiders?

Unit Assignment: Operations on Functions

Question 1

Determine the composite function ƒ o g and g o ƒ

For each composite function state the domain and range.

a) ƒ(x) = 3x² - 5x + 6 and g(x) = x² + 3x

b)  ƒ(x) = 2^x and g(x) = 3-x

c) ƒ(x) = sin x and g(x) = x

Question 2

Given the functions ƒ(x) = 10^x and g (x) = 3X² + 10 and h(x)=x-1 what corn position of functions would result in the following:

a)  y = 3 (10^2x) + 10

b) y = 10^x - 1

c)  y = 3x² + 9

Question 3

Given g(x) = x² - 2 and f(x) = 1/2- x , find g^-1(x) , ƒ^-1(x), (goƒ)^-1(x)  and (f-¹o g-¹)(x) .

What can you conclude?

Question 4

Suppose you need to choose between two car rental companies. You plan on driving for 6 hours at a constant speed of 100km/h.

Company 1 charges $1.50/km and a daily fee of $45.
Company 2 charges $1.65/km and a daily fee of $40.

What is the ifference in price between the two companies? Use composite functions to determine your answer.

Question 5

From the following chart choose two of the four function pairs.

i) Explain the meaning of y= h(g(x));

ii) Give a real life example of y = h(g(x))

g(x)	h(x)
Height is a function of Time	Air Pressure is a function of Height
Depth is a function of Time	Volume is a function of Depth
Sum of the Angles of a regular polygon is a function of the Number of Sides	Size of each Angle is a function of the Sum of the Angles of a regular polygon
Radius is a function of Time	Volume is a function of Radius

Question 6

Suppose a rock dropped into a pond creating a circular ripple travelling at a speed of 80 cm/s in an outward direction.

a) Let r be the radius of the circle. Express r as a function of time, t, in seconds.

b) If A is the area of this circle as a function of the radius, find A o r and interpret it.

Question 7

Does the composition of functions display the commutative property? Give an example of each case to illustrate your answer.

Mid Unit Asisgnment: Dragon's Den

The 'Dragon's Den' is a reality television show where entrepreneurs pitch their business ideas in the hopes of securing an investment from the team of investors also known as "The Dragons".

In this activity, you are an entrepreneur pitching your new idea to the Dragon's Den. You will need to create one of the following options to pitch your idea:

• Video

• Website

• PowerPoint

• Written Report

You must include all calculations and graphs in whichever method you choose.

Complete the following tasks (Questions 1 - 7) for your assignment:

Question 1

Watch this clip from Dragon's Den to familiarize yourself with the concept of pitching your product to investors.

Question 2

Think of a product you would like to invent. Some of the most successful pitches on dragons den are products created for everyday living that will make consumers lives easier. Have you ever been completing a task and thought there has to be an easier way? Well now is the time to explore that idea! If you are having a hard time coming up with an idea go to the Dragon's Den website. You may choose to use one of these products from the show or a similar one for your project. Choose an item that will retail between $5-$10.

Question 3

Now you will need to research how much your idea will cost per month and create a function in the form of c(x)= mx+b to represent it. Here are the two different monthly costs for operating your new business. Choose the most appropriate fit for your product:

a) Operating and producing from home, C(x)=mx, where m is the cost of your material and x is the number of items produced

b) Operating and producing from a storefront or factor: C(x)=mx+b, where m is the cost of your material and x is the number of items produced and b is your overhead costs such as rent

Question 4

Choose a selling price between $5-$10. Suppose on an average month you sell 500 items. For every $0.15 increase in your price you sell 10 less items.

a) Find a function for Revenue, with respect to the number of price increases. Your function will be R(x) = (number of products sold) x (price). It is important to incorporate that for every $0.15 in your price you sell 10 less items.

[Hint: First find a function for the number products sold, and a function for the price of the item.]

b) Provide a graph for your Revenue Function.

c) Determine the roots of R(x) and interpret them in the context of the question.

d) Determine the maximum or minimum values of R(x) and interpret them in the context of the question.

e) Determine the domain and range of and interpret them in the context of the question

f) Now create a revenue function with respect to the number of items sold and the new selling price.

Question 5

Using your Cost and Revenue functions, find the profit function, P(s)=R(x)—c(x).

Provide all of your calculations and a graph of your profit function.

Question 6

Now that you have your new product and all your calculations complete, it is time to create your pitch to The Dragon's. Remember you are trying to get them to invest in your product so you will want to include all the selling points from your calculations (such as your maximum profit).

You must include all calculations and graphs in whichever method you choose to present your pitch.

Question 7

Write a short reflection on this assignment. Were your results realistic?

Were your results realistic? What did you learn from this assignment? What was easy and what was more difficult?

Unit Assignment: Trignomatric Functions and Graphs

Question 1

For each of the following functions, state
• the domain;
• the range;
• the minimum and maximum values;
• the period;
• the phase shift;
• and the amplitude.

a) ƒ(x) = -2cos(3x-Π/4) +1

b) ƒ(x) =1/3sin (5x+Π)-1/2

Question 2 

Describe the transformations in each graph.

Sketch the graphs of the following functions by hand, using transformations. Show your work (show how the transformations map from the base function to the transformed function) for the graph in addition to listing the information.

Graph values from 0 ≤ x ≤ 2Π

a) ƒ(x) = sin(3x +3Π)

b) ƒ(x) = cos(1/2x - Π/4)+ 1

Question 3

For each of the graphs below, create a function of the form f (x) = a cos (k (x - d)) + c

or ƒ(x) = a sin (k (x - d)) c.

Show all of your calculations.

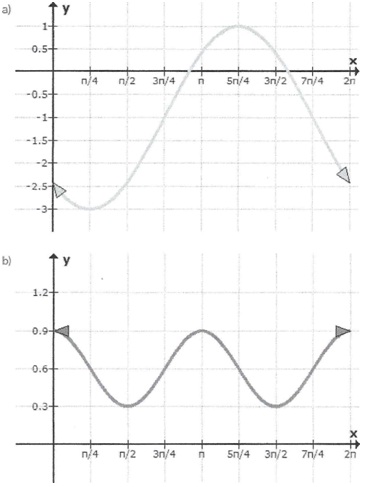
Question 4

On a particular lake, the difference between high and low tide is 6 hours. At low tide, 6 a.m., a student measures a 1.4 m distance from the dock she is standing on, down to the water. two hours later, she measures the distance from the dock down to the water to be 1.29 m. At 9 a.m., the distance is 1.175 m down to the water.

a)  Determine the function for the distance from the dock down to the water with respect to the number of hours since midnight.

b) Determine the distance to the water at 4:30 a.m. and 1:45 p.m.