Reference no: EM132264456

Question 1.

Recall the following "Baby" Master Theorem that we proved in class:

"Baby" Master Theorem: Let a > 0, b > 1 and d > 0 be constants. Then the solutions of a recurrence of the form

T(n) = aT (n/b) + Θ(n^d),

where T(n) is a constant for all small enough n, is

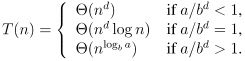
Apply this theorem to solve the recurrences in (a) - (f) below, where T(n) is constant for n ≤ 2. For each recurrence, justify how you apply the theorem (what are the values of a, b, d and which case applies), and express the solution in the 00 notation. (Note: 4 points for each of (a)-(f).)

(a) T(n) = 4T (n/2) + n².
(b) T (n) = 2T(7n/10) + n³.
(c) T(n) = 7T(n/3)+n.
(d) T(n) = 6T (n/4) + n√n.
(e) T (n) = 5T(n/9) + √n.
(f) T(n) = 3T(n/27) + ³√n.

Question 2.

Textbook Exercise 4.5-2 (page 97). You need to justify your answer.

Question 3.

Suppose that T(n) is a constant for n ≤ 2. Solve the following recurrences for T(n) and express the solutions in the Θ() notation.
(a) T (n) = T (n - 2) + n³.
(b) T (n) = 3T (n/3) + nlog²n.

Question 4.

Consider the recurrence T (n) given by

T (n) = 2T (n/2) + lg n,

where T (n) = 0 when n = 1.

(a) Solve T(n) using substitution with enhanced induction hypothesis as discussed in the Text¬book page 85.

(b) Solve T(n) by changing variables as discussed in the Textbook page 86 (starting with setting lg n = m) and repeated unfolding as discussed in the class. You should derive the exact expres¬sion for T (n).

Question 5.

Consider the deterministic quick selection algorithm (the algorithm SELECT in the Textbook, to find the k-th smallest item from a set of n unsorted items in 0 (n) worst-case time for any given integer k ∈ [1, n]) . Suppose we modify the algorithm so that the items are divided into groups of 9 (rather than groups of 5). Does the algorithm still run in worst-case linear time? Give a new recurrence for the worst-case running time T (n) , and solve T (n) and express it in terms of an asymptotic bound, i.e., either show that T (n) = O(n) , or show that T (n) = ω(n) .

Question 6.
Let x₁, x₂, .... , x_n, be an unsorted sequence of real numbers (each of which can be positive, neg-ative, or 0), where n > 1. Design and analyze a divide-and-conquer algorithm to find the sub-sequence of consecutive elements such that the product of the numbers in it is maximum over all consecutive subsequences. Here the "subsequence" must have length at least 1; i.e., it must be non-empty. Your algorithm should run in 0 (n log n) time.