Reference no: EM133074036

Question 1: Consider the flow network drawn in the figure below, with a starting flow f in blue (assume all edges without a blue number have flow 0). Starting with the flow f, simulate the Ford-Fulkerson

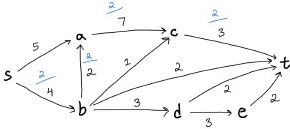
Figure 1: Black numbers are capacities, blue numbers are flow.

algorithm to find a maximum flow on this network. A complete answer will contain a list of successive augmenting paths and, for each augmenting path chosen, a picture of the new flow network after augmenting the flow along that path. Finally, list every minimum capacity cut on this network.

Question 2: Suppose that G is a flow network such that every edge in G has the same capacity d. Construct an algorithm that outputs a maximum flow on G in 0 (|V||E|) time (note the run time does not depend on d).

Question 3: Let G = (V, E) be any flow network with edge capacities c(e), let U be any minimum capacity s-t cut in G, and let (u, v) ∈ E be any edge such that u ∈ U, v 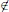U. Prove that in any maximum flow f on G, f (u, v) = c(u,v) (that is, the edge (u, v) is fully saturated with flow).

Question 4: You are planning seating for a wedding, and would like to mix-and-match people from different families so that everyone can mingle. However, you only have a limited number of tables which can each seat a limited number of people. To solve this problem, you will come up with a general algorithm that can either match people to tables so that no two people from the same family are seated at the same table, or determine if it is impossible to do so.

The input to the algorithm will be the following. You are given a list of n positive integers f₁,...., f_n, where f_i is the number of people in the ith family, as well as m positive integers t₁,t₂ t_m where t_j represents the number of people that can be seated at table j. Give an efficient algorithm that will decide if it is possible to seat everyone at the tables so that no two members from the same family are seated at the same table.

Question 5. The Montreal Jazz Fest is on this summer, and you know what that means: it's time to make some money by selling bootleg recordings! You have a list of the events that are being played at the Jazz Fest, namely: their start times, the length of each event, and also the location at which the event is playing. However, it may be impossible to attend every event in order to make a bootleg recording, so, you will have to hire some accomplices to help you out Naturally, in order to maximize your profit, you would prefer to figure out the minimum number of people you need to hire in order to cover every single event. Being a computer scientist, you decide to come up with an algorithm to solve the job.

Give an efficient algorithm for the following problem. As input, you receive a list of locations L₁,....L_m and a list of events E₁...E₂,...En occuring on a single day, where each event E_i is specified by a start time an event length 4, and the location L_i that the event occurs at (you may assume that all events are scheduled so that no two overlap at the same location). You also receive a list of integers tii for each pair of locations L_i, L_j that represents the travel time from location i to location j in minutes. Your algorithm should determine the fewest number of people required to attend all of the events, and output an event schedule for each of the persons.

Question 6. Suppose you have a computer with n applications. Let's (imaginatively) call these applications A₁, A₂,.....A_n. You would like to update some of these applications to their latest and greatest versionst; however, there may be new problems introduced between the newly updated applications and legacy software. Your goal is to figure out how to choose a subset of applications so that your overall benefit is maximized.

As input, you receive a list of applications A₁, ..... A_n and subset S ⊆ [n] of applications that have available updates. For each i ∈ S, the input contains a positive integer bi representing the benefit you get by updating that application. Finally, for each (unordered) pair of applications Ai, Aj, the input contains a positive integer x_ij which represents the penalty you have to pay if you update one application and not the other application. Design an efficient algorithm that chooses a subset U ⊆ S of the applications to update in order to maximize the quantity.

∑_i∈U b_i - ∑_i∈U,i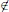U x_ij