Reference no: EM132268218

Assignment -

Description - Suppose we are running a bed manufacturing company. There are several different types of bed of various dimensions (length and width) that we can produce. To decide which beds we should produce, we run a market survey asking people what dimensions they require in a bed (i.e. the minimum length and the minimum width they need). We say that a person is compatible with a bed type if its length is at least that person's length requirement, and its width is at least that person's width requirement. The compatibility of a bed type is the number of persons compatible with it. Our goal is to determine efficiently the compatibility of every bed type.

We now state the problem more formally. Suppose we have n bed types, and surveyed n persons. Let B = {b₁, . . . , b_n} be a set of n points in 2-dimensional space representing the dimensions of the bed types. We write b_i = (b_i(x), b_i(y)) with b_i(x) representing the length of bed type i and b_i(y) its width. Similarly, we represent the requirements of the n persons with P = {p₁, . . . , p_n}, a set of n points in 2-dimensional space, and we also write p_j = (p_j(x), p_j(y)) where p_j(x) and p_j(y) are person j's length and width requirements, respectively.

Point b_i is compatible with point p_j if and only if b_i(x) ≥ p_j(x) and b_i(y) ≥ p_j(y). The compatibility of b_i is the number of points of P that it is compatible with and we write comp(b_i) = k if it is compatible with k points of p. See Figure 1 for an illustration.

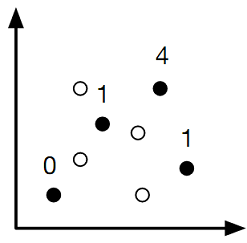
Figure 1: The solid circles represent points in B and the hollow circles represent points in P. The numbers represent the compatibility of each points in B.

Your task is to design an algorithm that computes the compatibility of every point in B.

Task 1: 1-dimensional case

We will start with the simpler 1-dimensional case, that is, P = {p₁, . . . , p_n} and B = {b₁, . . . , b_n} are points in 1-dimensional space (multiple points may have the same value). Your task is to design an O(n log n) time algorithm that computes the compatibility of each point in B with P.

(a) Description of how your algorithm works ("in plain English").

(b) Argue why your algorithm is correct.

(c) Prove an upper bound on the time complexity of your algorithm.

(d) Implement your algorithm (in Ed) (see the appendices for the data formats).

Task 2: 2-dimensional case

Consider the same problem in 2D, that is, let P = {p₁, . . . , p_n} and B = {b₁, . . . , b_n} be a set of points in 2-dimensional space, where each point p_i is a 2-tuple p_j = (p_j(x), p_j(y)) and b_i = (b_i(x), b_i(y)). The task is to solve this problem using a divide-and-conquer approach. A divide and conquer algorithm works by recursively breaking down a problem into two (or more) sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then merged to give a solution to the original problem. For full marks on this question the algorithm is required to run in O(n log n) time.

We will start with the merge step.

(a) Merge step - Consider a vertical line L. Suppose the line splits P into two sets P₁ = {p₁, . . . , p_l} and P₂ = {q₁, . . . , q_n-l}, where P₁ lies to the left of L and P₂ lies to its right. Similarly, it also splits B into two sets B₁ = {b₁, . . . , b_m} and B₂ = {c₁, . . . , c_n-m}. We will also assume that the sets in P₁ and P₂, B₁ and B₂ are ordered from bottom to top (in case of a tie the points are ordered with respect to increasing x-coordinates). Assume that the problem has been solved for (P₁, B₁) and (P₂, B₂), respectively. That is, the compatibility of each points in B₁ has been computed with respect to P1 and the compatibility of each point in B₂ has been computed with respect to P₂. Your task is to combine the two solutions into one solution for P = P₁ ∪ P₂ and B = B₁ ∪ B₂ in O(n) time. An example is shown in Fig. 2.

(i) Description of how your algorithm works ("in plain English").

(ii) Argue why your algorithm is correct.

(iii) Prove an upper bound on the time complexity of your algorithm.

(iv) Implement your algorithm (in Ed) (see the appendices for the data formats).

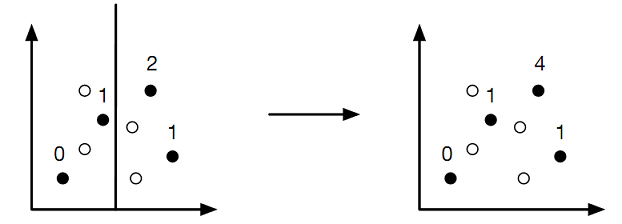
Figure 2: The point sets P₁, B₁ are separated from P₂, B₂ by a vertical line. The merge step merges the input data into the compatibility of all the points in B = B₁ ∪ B₂ with respect to points P = P₁ ∪ P₂.

(b) The final task is to use the merge step algorithm from (a) to construct a divide-and-conquer algorithm for the problem.

(i) Description of how your algorithm works ("in plain English").

(ii) Argue why your algorithm is correct.

(iii) Prove an upper bound on the time complexity of your (entire) algorithm.

(iv) Implement your algorithm (in Ed) (see the appendices for the data formats).

Attachment:- Assignment File.rar