Reference no: EM132608213

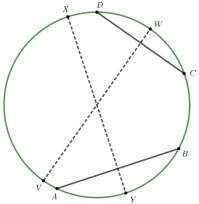
Question 1. Let XY and VW be perpendicular bisectors of the chords they intersect. What can you conclude about the center of the circle? Explain your reasoning.

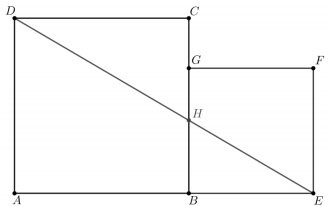
Question 2. The area of the square ABCD is 49 m² and the area of the square BEFG is 25 m². Find the length of the line segment DE. Find the ratio GH:BH. Round the answers to the nearest tenth.

Question 3. The cube ABCDEFGH is given. The volume of the given cube is V. Find the volume of the intersection of the tetrahedrons AFCH and EBGD. Describe the solid obtained by intersecting the tetrahedrons.

Question 4. Let a and b be lengths of the base edges of the trapezoid, where a > b. Prove given statements:
a) The length of the line segment connecting the midpoints of the legs of trapezoid is a+b/2
b) The length of the line segment parallel to the base edges of the trapezoid, that divides the trapezoid into two trapezoids with equal areas, is √a²+ b²/2
c) The length of the line segment parallel to the base edges of the trapezoid, that divides the trapezoid into two similar trapezoids, is √ab
d) The length of the line segment parallel to the base edges of the trapezoid, passing through the intersection of the diagonals of the tra-pezoid, is 2/(1/a +1/b)

The lengths given above have specific names. How are four given lengths called?

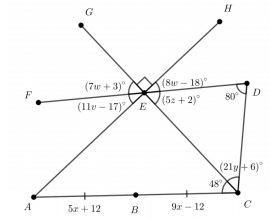
Question 5. Find the unknown values. State which rule or theorem is used to find each of the values.