Reference no: EM132726412

Question 1: Define Forest in the context of graph theory.

Question 2: Draw a Forest with (a + 6) number of vertices and (a + 2) edges where a is the last digit of your id number. Upload the diagram of forest as a clear image/pdf which is less than 20 mb in size.

Question 3: Find the preorder search output of the following binary tree, where a=15, b=6, c=1 6, d=9, e=21. Simplify the expression by using Prefix notation method.

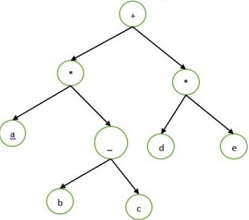
 a. Prefix simplification answer = 444  b. None of them are correct answers
 c. 9
 d. Preorder search answer: + * 15 - 6 16 *9 21
 e. Prefix simplification answer = 39
 f. Preorder search answer: + * 15 + 6 9 *16 21

Question 4: Let A= { 6,7,8,9 } and B. { 10,81,100 }. Let R be a relation defined from A to B such that R = { (x, y) ∈ AxB|
x² < y }. Choose the elements best roster form of R from the following
 a. None of the given answers
 b. R= i( (6,81), {6,100), (7,81), (7,100), (8,81), (8,100), (9,100) )
 e. R= ( (6,36), (6,80), (8,49), (10,100), (8,72), (8,100), (8,121) }
 d. R= i( (6,81), {6,121), {7,121), (10,100), (10,81), (6,100), (9,81) }

Question 5: Let A= { 7,8,9,10 } and B. { 11,100,121 }. Let R be a relation defined from A to B such that R = { (x, y) ∈ A x B | x² < y }. Choose the domain and range of the relation. ( Choose one answer for Domain and one answer for Range)
 a. Range is not given
 b. Domain =( 100, 81,9,10
 c. Range ={ 110, 77 }
 d. Domain =( 100, 99,7,7 }
 e. Domain is not given
 f. Domain =( 7, 8,9,10
 g. Range =( 49, 64,81 }
 h. Range =1100, 121 }

Question 6: Let A= { 6,7,8,9 } and B= { 10,81,100 }. Let R be a relation defined from the set A to B such that R = { (x, y) ∈ A x B | x² < y }. Comment on the symmetric nature of R.
 a. R is an anti symetric relation
 b. ( (81,6) belongs to R
 c. R is a Symmetric relation
 d. All of them correct answers
 e. R is an asymmetric relation

Question 7: Let A= { 14,15,16,17 } and B= { 18,289,324 }. Let R be a relation defined from the set A to B such that R = {x, y) ∈ A x B | x² < y }. Comment on the reflexive nature of R.
 a. Relation R is neither reflexive nor irreflexive
 b. None of them are correct answer
 c. The relation R is an reflexive relation
 d. The relation R is an irreflexive relation
 e. (14,14) belongs to R

Question 8: Let A= { 10,11,12,13 } and B= { 14,169,196 }. Let R be a relation defined from A to B such that R = { (x, y) ∈ A x B | x² < y }. R is an Asymmetric relation. Say true or false
 a. False, (10, 1 69) belong to R but (169,10) not in R
 b. False, (169,10) belong to R but (10, 169) not in R
 c. False, (169,10) belong to R but (10, 100) not in R
 d. True, (169,10) belong to R but (10, 169) belongs to R

Question 9: Choose the best solve of the following recurrence relation from the options given below yn - 9y-1 + 20yn-2 = 0, where n > 2, m, n > 0.
 a. y_n = A (5)An + B (4)An
 b. y_n = A (6)An + B (3)An
 c. y_n = A (3)"n + B (5)'n
 d. y_n = A (9)"ni - B (7)An

Question 10: If yn = A(4)n B(13)n is the general solution of the recurrence relation yn - 17y-1 + 52yn-2 = 0, where n > 2 then the suitable value of A and B. Given that the initial value are y0 = 8, y1 = 3.
 a. A=11.3; B=-6.8
 b. A=11.2; B=-7.2
 c. A=2; B=-4
 d. A=-3.4; B=-16.8

Question 11: If = A(7)n + B(5)n +C(3)n is the general solution of the following recurrence relation Yn - 12Yn-1 + 35Yn-2 = 5(3)n then choose the suitable suitable value of C from the following
 a. C=0,6
 b. C=5.6
 c. 0=0.7
 d. None of the given answers
 e. 0=0.9

Question 12: Let G. R be a group and * be a binary operator defined on G such that x * y = x + y + 21, then choose the identity of G from the following
 a. e=0.4
 b. e=6
 c. e=-21
 d. e=9
Question 13: Let G. R[(real number set) - (-0.14285714285714)] be a group and * be a binary operator defined on G such that x*y=x±y± 7xy, then choose the identity of G from the following
m a. e=0
m b. e=-0.14
m c. e= 14
m d. Answer not given

Question 14: Let G. R ( real numbers) be a group and * be a binary operator defined on G such that x * y = xy/11, then choose the inverse element of 10∈R
 a. None of the given answers
 b. Inverse element of 10.00 is 0.91
 c. Inverse element of 10.00 is 12.10
 d. Inverse element of 10.00 is 1.33

Question 15: If G (*,mod 20) is a group where G={[4],[8],[12],[16]} then find the inverse element of [12]∈G.
 a. 12
 b. 8
 c. 8
 d.4

Question 16: Let G be a group representing the fourth root of unity under the binary operator * defined on G such that x * y = xy, then choose the order of the element i ∈ C
Answer:

Question 17: Download the Quiz question paper from Moodie and answer it. With all the required steps submit the answer in a neatly typed word file in the Turnitin link on or before the due date. Answers given in the Moodle will be taken valid only if the necessary steps are given in the Turnitin submission. Add atleast five references and include citations in appropriate places in your assignment work. Follow CU Harvard referencing style.

Question 18: Write a brief note about the status of your Discrete Mathematics Mooc course with evidence (screenshot) of completion and progress made after the assignment 01.