Reference no: EM132321545

COMPULSORY QUESTION   

1. a) Find the limits of the following sequences as n →∞, and justify your results by quoting relevant standard limits and rules for limits:

(i) an := ((n²-1) /n!)

(ii) an := 5ⁿ3^-n2

b) Suppose a_n→a and b_n →6 as n →∞. Show that the sequence cⁿ := aⁿ+ 6ⁿ is convergent and converges to a + b as n→∞.

C) Is the series[_n=1∑^∞ ((5ⁿ-2ⁿ)/(7n+2ⁿ))], absolutely convergent, conditionally convergent or not convergent at all? Justify your claim by quoting relevant convergence and comparison tests.

d) Prove that if _n=1∑^∞a_n ,is absolutely convergent then it is convergent.

e) Let E ⊂ R. Suppose that ƒ: E →R is continuous. at c ∈ E. Show that E R, where |ƒ|:(x) = |ƒ(x)|, is also continuous at c ∈ E.

f)  Let E ⊂ R. State what it means for a function ƒ: E→ R to be discontinuous at a point c ∈ E.

g) Let ƒ:R→R be given by

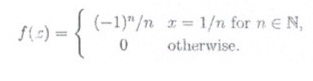
Show that ƒ is continuous at 0, and discontinuous at 1.

h) Give the definition for ƒ: (a, b) → R to be differentiable at a point x₀ ∈(a, b).

i)  (1) Prove that ƒ(x)= x³ is differentiable at every x E R.

(2) Prove that

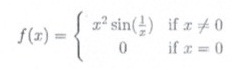
is differentiable at 0.

j)  Suppose ƒ: |0,1|→ R It is differentiable and c ∈ (0, 1) is a local maximum of ƒ. Show that ƒ'(c) = 0.

OPTIONAL QUESTIONS

2. a) Let l ∈ R, and ƒ:R → R. Define what it means for f (x)→l as x →+∞.

b) Define what it means for M∈ R to be an upper bound for a function ƒ:R → R.

c) Let ƒ: [a, b]→ R be continuous on [a, b]. Apply the Bolzano-Weierstrass Theorem to prove that there exists an upper bound for ƒ on [a,b]

d) State the Extreme Value Theorem.

e) Suppose that g: R → R is continuous on R and that there exist α, β ∈ R it such that g(x)→ α as x→ +∞ and g(x)→β as x→ -∞. Prove that g is bounded on R.

f) Let P: R → R be a polynomial of degree 2n -1 for some n ∈ N. Define. Q: R → R by Q(x) = P(x)/(1 +x²ⁿ). Prove that Q is bounded on R.

3. a) Define what it means for a function ƒ: [a, b]→ R to be continuous at a point c ∈[a,b]

b) Let ƒ: [a, b]→ R be continuous at c ∈[a,b], and suppose (x_n) is a sequence in [a, b] such that x_n→ c as n→∞. Prove that ƒ(x_n) →ƒ(c) as n→∞ .

c) State the Intermediate Value Theorem.

d) Define what it means for a function ƒ: [a, b]→ R to be strictly increasing.

The remainder of this question constructs a proof of the Intermediate Value Theorem in the special case of a strictly increasing function.

Let ƒ: [0, 1]→ R be continuous and strictly increasing on [0,1] and suppose ƒ(0) < 0 < ƒ(1). We inductively define sequences (a_n) and (bn) in [0,1] such that an≤ bn for all n E N, as follows.

Define a₁ = 0 and b₁= 1. Suppose that for n ∈ N the points a_n, b_n, ∈ [0, 1] have been defined such that a_n ≤ b_n and f (a_n) ≤ 0 ≤ f(b_n).

Then

• if f (a_n) = 0, we define a_n+1= an and b_n+1= a_n; and

• if f (b_n) = 0, we define a_n+1 = bn and b_n+1=b_n.

Otherwise ƒ (a_n) < 0 < ƒ (b_n). In this case

• if ƒ((b_n +a_n)/2) ≥ 0, we define a_n+1 and bn+1 = (b_n + a_n)/2; and

• if ƒ((b_n +a_n)/2) < 0, we define a_n+1 =(b_n + a_n)/2 and b_n+1=b_n.

Any results about sequences may be used without proof providing they arc clearly stated.

e) Show that ƒ(a_n) ≤0≤1(b_n) for all n ∈ N.

f) Show that there exists to x₀ ∈ [0,1] such that an→x₀ and b_n→x₀ as n→∞.

g) Deduce that ƒ(x₀) = 0.

h) Now suppose that g: [0,1]→R is continuous and strictly increasing on [0, 1], and ξ∈ R is such that g(0)<ξ< g(I). Show that there exists y₀∈ [0,1] such that g(y₀)=ξ.

i) Now suppose that [a, b] ⊆ R and h: [a,b]→R is continuous and strictly increasing on (a,b), and that η∈R is such that h(a)<η< h(b). Show that there exists z₀ ∈ [a,b] such that h(z₀) = n. (Hint: you may assume that the function Φ: [0,1]→(a,b) given by Φ(x) = a + (b-a)x is continuous and strictly increasing.)

4. a) State Rolle's Theorem.

b) Let ƒ: [0,Π/2]→R be defined by ƒ(x) = x_3-1+sin(x). Show that there is a  unique c₁ ∈ (0,Π/2) for which ƒ(c₁) = 0.

c) State the Mean Value Theorem.

d) Suppose g:[0,Π/2]→F: is differentiable and satisfies g(0)= 0 and y(Π/2) a 31. If h= ƒ+ g, with ƒ defined as in part b) above, that there is some c₂ ∈ (0,Π/2) with h'(c₂) > 22.

e) Compute the limits:

(i) lim_x→∞( x³e^-x2)

⁽ⁱⁱ⁾ lim_x→1 (cos(xⁿ-1)-1/sin(Π/x))

where n∈N, briefly explaning your procedure and role of any theorems you apply in each case.

5. a) (i) Compute the Taylor series of ƒ(x)= (1/(2-x)) about x₀ = 0.

(ii) What is the radius of convergence of the Taylor series you computed?

c) Suppose ƒ∈C²(|a,b|) is 3-times differentiable on (a,b) and γ∈R is defined by
    ƒ(b)= ƒ(a)+ƒ'(a) (b - a) +ƒⁿ(a)/2)-(b-a)² +γ(b - a)³.

Let g: [a,b]→R be defined by

g(x)=ƒ(b)-(ƒ(x) +ƒ'(x)(b - x) +(ƒ^"(x)/2(b-x)²)-γ(b-x))³

Show that g(a) = g(b) = 0.

Given that g'(c) = 0 for some c ∈ (a, b), compute the value of γ in terms of the third derivative of ƒ.

d) If ƒ: R→ R is n-time, differentiable and a∈ R define the Taylor polynomial P_n,a of ƒ of degree n at a.

c) Compute the degree r, Taylor polynomial P_3,a of h(x) = cos(x) around x₀ = 0. Find some δ ∈ 0 such that |h(x)- P₃,₃(x)|< 1/10000 for every x ∈ (-δ,δ) and justify your answer.